
(12分)设各项均为正数的数列 的前
的前 项和为
项和为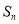 ,满足
,满足
且 构成等比数列.
构成等比数列.
(Ⅰ)证明: ;
;
(Ⅱ)求数列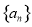 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数 ,有
,有 .
.
(Ⅰ)详见解析;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)对于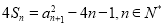 ,令
,令 即可证明;(Ⅱ)由已知所给的递推式
即可证明;(Ⅱ)由已知所给的递推式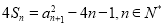 含有
含有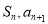 ,考虑用公式
,考虑用公式 ,得到
,得到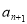 和
和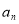 的递推式,构造等差数列,进而求出数列的通项;(Ⅲ)因为
的递推式,构造等差数列,进而求出数列的通项;(Ⅲ)因为 是一个分式,常通过裂项相消法逐项相消,然后再通过放缩,得出结论.
是一个分式,常通过裂项相消法逐项相消,然后再通过放缩,得出结论.
试题解析:(Ⅰ)证明:由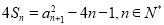 ,得
,得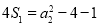 ,即
,即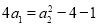 ,
,
所以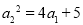 .因为
.因为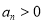 ,所以
,所以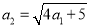 ;
;
(Ⅱ)【解析】 (1)
(1)
 当
当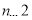 时,
时,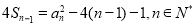 (2)
(2)
由(1)-(2)得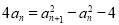 ,即
,即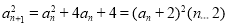

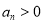 ,
,
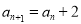 ,即
,即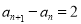
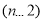 ,(下面需验证
,(下面需验证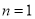 时的情况)
时的情况)

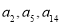 成等比数列,所以
成等比数列,所以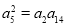 ,即
,即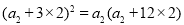 ,解得
,解得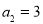
又由(1)知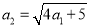 ,
,
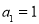 ,
,
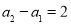 ,
,
综上知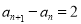 (
(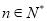 );
);
 数列
数列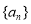 是一个首项为1,公差为2的等差数列.
是一个首项为1,公差为2的等差数列.
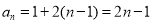 ,
,
 数列
数列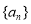 的通项公式为
的通项公式为 ;
;
(Ⅲ)证明:由(2)知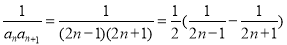 ,
,

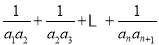
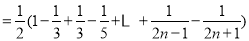
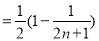
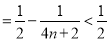 .
.
考点:数列的递推公式、通项公式、;等比中项、等差数列的概念;裂项相消法求数列的前 项和;放缩法证明不等式等知识.
项和;放缩法证明不等式等知识.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:选择题
各项不为零的等差数列 中,
中, ,数列
,数列 是等比数列,且
是等比数列,且 ,则
,则 ( )
( )
A、2 B、4 C、8 D、16
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期10月模块考试数学试卷(解析版) 题型:选择题
设数列 是以2为首项,1为公差的等差数列,
是以2为首项,1为公差的等差数列, 是以1为首项,2为公比的等比数列,则
是以1为首项,2为公比的等比数列,则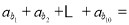 ( )
( )
A.1033 B.2057 C.1034 D.2058
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期10月模块考试数学试卷(解析版) 题型:选择题
设 是等差数列,
是等差数列, 为等比数列,其公比q≠1, 且
为等比数列,其公比q≠1, 且 (i=1、2、3 …n)若
(i=1、2、3 …n)若 ,
, 则( )
则( )
A. B.
B. C.
C. D.
D. 或
或 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省分校高二10月月考数学试卷(解析版) 题型:选择题
一个只有有限项的等差数列,它的前5项的和为34,最后5项的和为146,所有项的和为234,则它的第7项等于 ( )
A.22 B.21 C.19 D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com