
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 由已知条件2a=3b,结合正弦定理推知3sinB=2sinA,故sinA=$\frac{3}{2}$sinB,将其代入所求的代数式进行求值即可.
解答 解:∵在△ABC中,角A.B、C的对边分别为a,b,c,2a=3b,
∴由正弦定理得到:3sinB=2sinA,故sinA=$\frac{3}{2}$sinB,
∴$\frac{9si{n}^{2}B-si{n}^{2}A}{si{n}^{2}A}$=$\frac{9si{n}^{2}B-\frac{9}{4}si{n}^{2}B}{\frac{9}{4}si{n}^{2}B}$=3.
故选:B.
点评 本题考查三角形的正弦定理的运用,考查运算能力,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | y=1,y=x0 | B. | $y=x\;,\;y=\root{3}{x^3}$ | ||
| C. | $y=\sqrt{x-1}•\sqrt{x+1}\;,\;y=\sqrt{{x^2}-1}$ | D. | $y=|x|\;,\;y={(\sqrt{x})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-1,\frac{1}{2}})$ | B. | $({-∞,\frac{1}{2}})$ | C. | $({\frac{1}{2},2})$ | D. | $[{-1,\frac{1}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
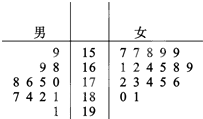 某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm
某部队为了在大阅兵中树立军队的良好形象,决定从参训的12名男兵和18名女兵中挑选出正式阅兵人员,这30名军人的身高如图:单位:cm查看答案和解析>>
科目:高中数学 来源: 题型:填空题
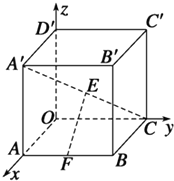 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com