
分析 求出f(x)的导数,问题转化为a≥$\frac{2}{x}$-2x,求出a≥0,求出g(x)的导数,结合函数的单调性求出a的范围即可.
解答 解:由f′(x)=$\frac{a}{x}$-$\frac{2}{{x}^{2}}$+2≥0,得:a≥$\frac{2}{x}$-2x,
设h(x)=$\frac{2}{x}$-2x,则a≥h(x)max=h(1)=0,
g(x)=$\frac{f(x)}{x}$=$\frac{alnx}{x}$+$\frac{2}{{x}^{2}}$+2,
g′(x)=$\frac{ax-axlnx-4}{{x}^{3}}$,(x>1),
设t(x)=ax-axlnx-4,t′(x)=-alnx,
a≥0时,t′(x)≤0,t(x)在[1,+∞)递减,
故t(x)max=t(1)=a-4≤0,
综上,0≤a≤4.
故答案为:[0,4].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
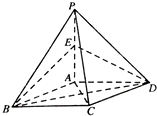 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-2\sqrt{2},2\sqrt{2})$ | B. | (-2,2) | C. | (-1,1) | D. | $(-\sqrt{3},\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
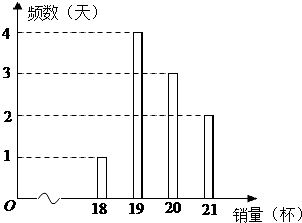 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com