
分析 (1)由A,C坐标,代入两点式,可得边AC所在直线的方程;
(2)求出D点坐标,代入截距式,可得BC边上的中线AD所在直线的方程;
(3)求出AE的斜率,代入点斜式,可得BC边上的高AE所在直线的方程.
解答 解:(1)∵A(-3,0),C(-2,3),
故边AC所在直线的方程为:$\frac{x+3}{-2+3}=\frac{y}{3}$,
即3x-y+9=0,
(2)BC边上的中点D(0,2),
故BC边上的中线AD所在直线的方程为$\frac{x}{-3}+\frac{y}{2}=1$,
即2x-3y+6=0,
(3)BC边斜率k=$\frac{1-3}{2+2}$=-$\frac{1}{2}$,
故BC边上的高AE的斜率k=2,
故BC边上的高AE所在直线的方程为:y=2(x+3),
即2x-y+6=0.
点评 本题考查的知识点是直线方程,根据已知条件选取合适的直线表示方法,是解答的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
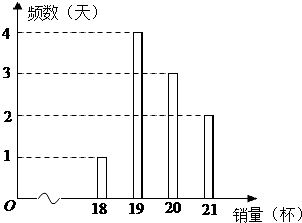 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com