
分析 先求出正四面体内切球的半径和体积,结合几何概型的概率公式进行计算即可
解答  解:设正四面体S-ABCD如图所示,
解:设正四面体S-ABCD如图所示,
可得它的内切球的球心0必定在高线SH上,
延长AH交BC于点D,则D为BC的中点,连结SD则内切球切SD于点E,连结AO,
∵H是正三角形ABC的中心,
∴AH:HD=2:1,
∵Rt△0AH∽Rt△DSH,
∴$\frac{OA}{OH}=\frac{DS}{DH}$=3,可得OA=30H=S0,
因此,SH=4OH,可得内切球的半径OH=$\frac{1}{4}$SH;
∵正四面体棱长为1,
∴Rt△SHD中,SD=$\frac{\sqrt{3}}{2}$,HD=$\frac{1}{3}$SD=$\frac{\sqrt{3}}{6}$,
可得SH=$\sqrt{S{D}^{2}-H{D}^{2}}$=$\frac{\sqrt{6}}{3}$,得内切球的半径r=OH=$\frac{1}{4}$×$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{6}}{12}$,
在棱长为1的正四面体内任取一点,则该点落在正四面体内切球内的概率为P=$\frac{{V}_{球}}{{V}_{四面体}}$=$\frac{\frac{4}{3}π{×(\frac{\sqrt{6}}{12})^{3}}^{\;}}{\frac{1}{3}×\frac{1}{2}×{1}^{2}×\frac{\sqrt{3}}{2}×\frac{\sqrt{6}}{3}}$=$\frac{3π}{18}$,
故答案为:$\frac{3π}{18}$.
点评 本题主要考查几何概型的概率的计算,根据条件求出内切球的半径和体积是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,f(x)=x0 | B. | f(x)=|x|,f(t)=$\sqrt{t^2}$ | ||
| C. | f(x)=$\frac{x^2-1}{x-1}$,g(x)=x+1 | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{x^2-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
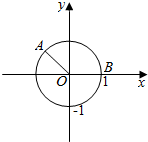 已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示
已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com