
分析 根据积分的运算法则进行求解即可.
解答 解:∵${∫}_{0}^{1}$exdx=e-1,${∫}_{0}^{1}$x2dx=$\frac{1}{3}$.
∴${∫}_{0}^{1}$(ex+x2)dx=${∫}_{0}^{1}$exdx+${∫}_{0}^{1}$x2dx=e-1+$\frac{1}{3}$=e-$\frac{2}{3}$;
(2)${∫}_{0}^{1}$(2ex-x2)dx=2${∫}_{0}^{1}$exdx-${∫}_{0}^{1}$x2dx=2(e-1)-$\frac{1}{3}$=2e-$\frac{7}{3}$..
点评 本题主要考查函数积分的计算,根据积分的运算法则是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$cosx | B. | -$\frac{\sqrt{2}}{2}$cosx | C. | -$\frac{\sqrt{2}}{2}$sinx | D. | $\frac{\sqrt{2}}{2}$sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
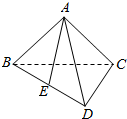 如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.
如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com