
【题目】如图所示,该几何体是由一个直三棱柱![]() 和一个正四棱锥
和一个正四棱锥![]() 组合而成,
组合而成, ![]() ,
, ![]() .
.
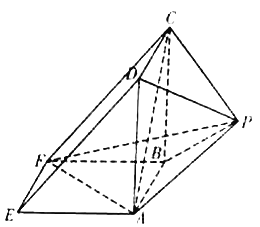
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求正四棱锥![]() 的高
的高![]() ,使得二面角
,使得二面角![]() 的余弦值是
的余弦值是![]() .
.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,其中
,其中![]()
![]() .
. ![]() 表示
表示![]()
![]() 中所有不同值的个数.
中所有不同值的个数.
(Ⅰ)若集合![]() ,求
,求![]() ;
;
(Ⅱ)若集合![]() ,求证:
,求证: ![]() 的值两两不同,并求
的值两两不同,并求![]() ;
;
(Ⅲ)求![]() 的最小值.(用含
的最小值.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,飞镖的标靶呈圆盘形,圆盘被10等分,按如图所示染色为Ⅰ、Ⅱ、Ⅲ三部分,某人依次将若干支飞镖投向标靶,如果每次投射都是相互独立的.
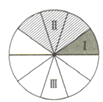
(1)如果他投向标靶的飞镖恰有2支且都击中标靶,同时每支飞镖击中标靶的任意位置都是等可能的,求“第Ⅰ部分被击中2次或第Ⅱ部分被击中2次”的概率;
(2)如果他投向标靶的飞镖恰有4支,且他投射1支飞镖,击中标靶的概率为![]() ,设
,设![]() 表示标靶被击中的次数,求
表示标靶被击中的次数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校初三年级有![]() 名学生,随机抽查了
名学生,随机抽查了![]() 名学生,测试
名学生,测试![]() 分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
分钟仰卧起坐的成绩(次数),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )

A. 该校初三年级学生![]() 分钟仰卧起坐的次数的中位数为
分钟仰卧起坐的次数的中位数为![]() 次
次
B. 该校初三年级学生![]() 分钟仰卧起坐的次数的众数为
分钟仰卧起坐的次数的众数为![]() 次
次
C. 该校初三年级学生![]() 分钟仰卧起坐的次数超过
分钟仰卧起坐的次数超过![]() 次的人数约有
次的人数约有![]() 人
人
D. 该校初三年级学生![]() 分钟仰卧起坐的次数少于
分钟仰卧起坐的次数少于![]() 次的人数约为
次的人数约为![]() 人.
人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量![]() 分布在
分布在![]() 内,且销售量
内,且销售量![]() 的分布频率
的分布频率
 .
.
(Ⅰ)求![]() 的值并估计销售量的平均数;
的值并估计销售量的平均数;
(Ⅱ)若销售量大于等于70,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取8天,再从这8天中随机抽取3天进行统计,设这3天来自![]() 个组,求随机变量
个组,求随机变量![]() 的分布列及数学期望(将频率视为概率).
的分布列及数学期望(将频率视为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com