
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
【答案】(1) ![]() .(2)证明见解析.
.(2)证明见解析.
【解析】试题分析:(1)转移法求轨迹:设所求动点坐标及相应已知动点坐标,利用条件列两种坐标关系,最后代入已知动点轨迹方程,化简可得所求轨迹方程;(2)证明直线过定点问题,一般方法是以算代证:即证![]() ,先设 P(m,n),则需证
,先设 P(m,n),则需证![]() ,即根据条件
,即根据条件![]() 可得
可得![]() ,而
,而![]() ,代入即得
,代入即得![]() .
.
试题解析:解:(1)设P(x,y),M(![]() ),则N(
),则N(![]() ),
),![]()
由![]() 得
得![]() .
.
因为M(![]() )在C上,所以
)在C上,所以![]() .
.
因此点P的轨迹为![]() .
.
由题意知F(-1,0),设Q(-3,t),P(m,n),则
![]() ,
,
![]() .
.
由![]() 得-3m-
得-3m-![]() +tn-
+tn-![]() =1,学&科网又由(1)知
=1,学&科网又由(1)知![]() ,故
,故
3+3m-tn=0.
所以![]() ,即
,即![]() .又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
.又过点P存在唯一直线垂直于OQ,所以过点P且垂直于OQ的直线l过C的左焦点F.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒成立的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(Ⅰ)根据频率分布表中的数据,写出![]() ,
, ![]() 的值.
的值.
(Ⅱ)某人从灯泡样品中随机地购买了![]() 个,求
个,求![]() 个灯泡中恰有一个是优等品的概率.
个灯泡中恰有一个是优等品的概率.
(Ⅲ)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰△ABC中,AB=AC=5,BC=6,将△ABC沿BC边上的高AD折成直二面角BADC,则三棱锥BACD的外接球的表面积为( )
A. 5π B. ![]()
C. 10π D. 34π
查看答案和解析>>
科目:高中数学 来源: 题型:
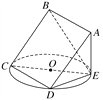
【题目】(2017·安徽名校阶段性测试)如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE=9.
(1)求证:平面ABE⊥平面ADE;
(2)求五面体ABCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知bcos2![]() +acos2
+acos2![]() =
=![]() c.
c.
(Ⅰ)求证:a,c,b成等差数列;
(Ⅱ)若C=![]() ,△ABC的面积为2
,△ABC的面积为2![]() ,求c.
,求c.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com