
分析 设B′(x,y),$[\begin{array}{l}{-1}&{0}\\{0}&{1}\end{array}]$$[\begin{array}{l}{-1}\\{2}\end{array}]$=$[\begin{array}{l}{1}\\{2}\end{array}]$,求得A′的坐标,写出向量$\overrightarrow{A′B}$,$\overrightarrow{A′B′}$,$[\begin{array}{l}{0}&{-1}\\{1}&{0}\end{array}]$$[\begin{array}{l}{2}\\{2}\end{array}]$=$[\begin{array}{l}{x-1}\\{y-2}\end{array}]$,即可求得x和y,求得点B′的坐标.
解答 解:设B′(x,y),
由题意可知:$[\begin{array}{l}{-1}&{0}\\{0}&{1}\end{array}]$$[\begin{array}{l}{-1}\\{2}\end{array}]$=$[\begin{array}{l}{1}\\{2}\end{array}]$,得A′(1,2),
则$\overrightarrow{A′B}$=(2,2),$\overrightarrow{A′B′}$=(x-1,y-2),
即旋转矩阵N=$[\begin{array}{l}{0}&{-1}\\{1}&{0}\end{array}]$,
则$[\begin{array}{l}{0}&{-1}\\{1}&{0}\end{array}]$$[\begin{array}{l}{2}\\{2}\end{array}]$=$[\begin{array}{l}{x-1}\\{y-2}\end{array}]$,
即$[\begin{array}{l}{-2}\\{2}\end{array}]$=$[\begin{array}{l}{x-1}\\{y-2}\end{array}]$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$,
所以B′的坐标为(-1,4).
点评 本题考查矩阵的变换,考查矩阵的乘法,考查点在变换下点的坐标的求法,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题p的逆命题为“若a>b,则lga>lgb”,且该命题为假命题 | |
| B. | 命题p的否命题为“若lga>lgb,则a≤b”,且该命题为真命题 | |
| C. | 命题p的逆否命题为“若a≤b,则lga≤lgb”,且该命题为真命题 | |
| D. | 命题p的否定为“若lga≤lgb,则a≤b”,且该命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
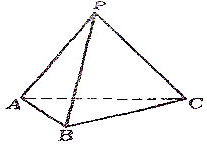 如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,
如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,已知圆C1:(x+3)2+y2=4和直线l:14x+8y-23=0.
在平面直角坐标系xOy中,已知圆C1:(x+3)2+y2=4和直线l:14x+8y-23=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com