Question

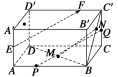
【题目】已知ABCD—A′B′C′D′是平行六面体．

(1)化简；

(2)设M是底面ABCD的中心，N是侧面BC C′ B′对角线B C′上的分点，设，试求α，β，γ的值．

Answer 1

【答案】（1）答案见解析；（2）.

【解析】

(1)方法一　取AA′的中点为E，取F为D′C′的一个三等分点(D′F＝D′C′)，由空间向量的运算法则可得 .

方法二　取AB的三等分点P使得，取CC′的中点Q，由空间向量的运算法则可得 .

(2)连结BD，则M为BD的中点，由空间向量的结论可得，则.

(1)方法一　取AA′的中点为E，则＝.

又＝，＝，取F为D′C′的一个三等分点(D′F＝D′C′)，

则＝.

∴＋＋＝＋＋＝.

方法二　取AB的三等分点P使得＝，

取CC′的中点Q，则＋＋

＝＋＋＝＋＋

＝＋＋＝.

(2)连结BD，则M为BD的中点，

＝＋＝＋＝ (＋)＋ (＋)

＝ (－＋)＋ (＋)＝＋＋.

∴α＝，β＝，γ＝.