
分析 利用复数的运算法则化简$\frac{z+1}{z+2}$=$\frac{{x}^{2}+3x+2+{y}^{2}+yi}{(x+2)^{2}+{y}^{2}}$,根据$\frac{z+1}{z+2}$的实部与虚部之比为$\sqrt{3}$,可得:$(x+\frac{3}{2})^{2}$+$(y-\frac{\sqrt{3}}{2})^{2}$=1.设$\frac{y}{x}$=k,则y=kx,根据直线与圆相切的充要条件可得:$\frac{|-\frac{3}{2}k-\frac{\sqrt{3}}{2}|}{\sqrt{1+{k}^{2}}}$≤1,化简解出即可得出.
解答 解:$\frac{z+1}{z+2}$=$\frac{x+yi+1}{x+yi+2}$=$\frac{(x+1+yi)(x+2-yi)}{(x+2+yi)(x+2-yi)}$=$\frac{{x}^{2}+3x+2+{y}^{2}+yi}{(x+2)^{2}+{y}^{2}}$,
∵$\frac{z+1}{z+2}$的实部与虚部之比为$\sqrt{3}$,∴x2+3x+2+y2=$\sqrt{3}$y,
配方为:$(x+\frac{3}{2})^{2}$+$(y-\frac{\sqrt{3}}{2})^{2}$=1.
设$\frac{y}{x}$=k,则y=kx,
则$\frac{|-\frac{3}{2}k-\frac{\sqrt{3}}{2}|}{\sqrt{1+{k}^{2}}}$≤1,化为5k2+6$\sqrt{3}$k-1≤0,
解得:$\frac{-3\sqrt{3}-4\sqrt{2}}{5}$≤k≤$\frac{-3\sqrt{3}+4\sqrt{2}}{5}$,
∴$\frac{y}{x}$的最大值为$\frac{-3\sqrt{3}+4\sqrt{2}}{5}$,
故答案为:$\frac{-3\sqrt{3}+4\sqrt{2}}{5}$.
点评 本题考查了复数的运算法则、圆的方程、直线与圆相切的充要条件、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{7}$ | B. | $\frac{7}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点 | B. | 准线 | C. | 焦距 | D. | 离心率 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (2,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
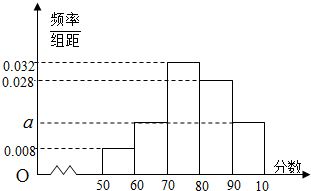 高二年级某班有50人,某次数学测验的分数在[50,100]内,现将这次数学测验的分数分成如下5个组:[50,60),[60,70),…,[90,100],绘制成如图所示的频率分布直方图,则图中的a值为( )
高二年级某班有50人,某次数学测验的分数在[50,100]内,现将这次数学测验的分数分成如下5个组:[50,60),[60,70),…,[90,100],绘制成如图所示的频率分布直方图,则图中的a值为( )| A. | 0.032 | B. | 0.16 | C. | 0.32 | D. | 0.016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com