考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)根据数列的递推公式直接进行求解即可求a8和a6的值;
(2)利用数学归纳法进行证明即可得到结论.
解答:
解:(1)因为a
7=4,a
n+1=
.
当n=6时,解得a
6=
,
当n=7时,解得a
8=
.
(2)类似计算得到,a
6=
,a
7=4,a
8=
,a
9=12,a
10=-8,a
11=-
.
由此猜想:
存在自然数m=10,使得当n≥10时,a
n<2;当n<10时,a
n>2.
证明:①首先验证,当n=1,2,3,…,9时,a
n>2.
由已知条件a
n+1=
,解得 a
n=
,
然后由a
7=4出发,计算这个数列的第6项到第1项:
a
6=
,a
5=
,a
4=
,a
3=
,a
2=
=
,a
1=
,
显然,当n<10时,a
n>2,
②再用数学归纳法证明:n≥10时,a
n<2.
①当n=10时,a
10=-8<2,猜想成立.
②假设当n=k (k≥10)时,猜想成立,即a
k<2,
那么当n=k+1时,有a
k+1-2=
-2=
,
由a
k<2,则a
k-2<0,7-a
k>0,
所以,a
k+1-2<0,即a
k+1<2成立.
根据①、②,当n≥10时,a
n<2.
因此,存在自然数m=10,使得当n≥10时,a
n<2;当n<10时,a
n>2.
点评:本题主要考查数列的递推公式的应用,根据数学归纳法是解决本题的关键.



 如图,在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.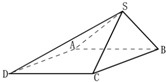 如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=
如图,设四棱锥S-ABCD的底面为菱形,且∠ABC=60°,AB=SC=2,SA=SB=