
下图是利用计算机作图软件在直角坐标平面 上绘制的一列抛物线和一列直线,在焦点为
上绘制的一列抛物线和一列直线,在焦点为 的抛物线列
的抛物线列 中,
中, 是首项和公比都为
是首项和公比都为 的等比数列,过
的等比数列,过 作斜率2的直线
作斜率2的直线 与
与 相交于
相交于 和
和 (
( 在
在 轴的上方,
轴的上方, 在
在 轴的下方).
轴的下方).
证明: 的斜率是定值;
的斜率是定值;
求 、
、 、
、 、
、 、
、 所在直线的方程;
所在直线的方程;
记 的面积为
的面积为 ,证明:数列
,证明:数列 是等比数列,并求所有这些三角形的面积的和.
是等比数列,并求所有这些三角形的面积的和.

(1)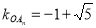 ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:
解题思路:(1)联立直线与抛物线方程,整理成关于 ,
, 的方程,进而求出
的方程,进而求出 的斜率;(2)利用直线的点斜式方程写出直线方程即可;(3)联立直线与抛物线方程,求弦长与点到直线的距离,进而求三角形的面积.
的斜率;(2)利用直线的点斜式方程写出直线方程即可;(3)联立直线与抛物线方程,求弦长与点到直线的距离,进而求三角形的面积.
规律总结:锥曲线的问题一般都有这样的特点:第一小题是基本的求方程问题,一般简单的利用定义和性质即可;后面几个小题一般来说综合性较强,用到的内容较多,大多数需要整体把握问题并且一般来说计算量很大,学生遇到这种问题就很棘手,有放弃的想法,所以处理这类问题一定要有耐心..
试题解析:(1)由已知得 ,抛物线焦点
,抛物线焦点 ,抛物线方程为
,抛物线方程为 ,直线
,直线 的方程为
的方程为 于是,抛物线
于是,抛物线 与直线
与直线 在
在 轴上方的交点
轴上方的交点 的坐标满足
的坐标满足 则有
则有
而直线 的斜率为
的斜率为 ,则
,则 解得
解得
又 点
点 在第一象限,则
在第一象限,则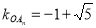 ;
;
直线方程为 ;
;
由 得
得 则
则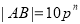 ,
,
而 到直线
到直线 的距离为
的距离为 ,
,
于是 的面积
的面积 ,
,
所以数列 是以
是以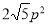 为首项,
为首项, 为公比的等比数列.由于
为公比的等比数列.由于 ,
,
所以所有三角形面积和为 .
.
考点:1.直线的方程;2.直线与抛物线的位置关系.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源:2015届云南省云龙县高二下学期期末考试试卷理科数学试卷(解析版) 题型:选择题
如图是一个几何体的三视图(尺寸的长度单位为 ),则它的体积是( )
),则它的体积是( ) .
.

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届云南省云龙县高二下学期期末考试试卷文科数学试卷(解析版) 题型:选择题
双曲线 与抛物线
与抛物线 有一个公共焦点
有一个公共焦点 ,双曲线上过点
,双曲线上过点 且垂直实
且垂直实
轴的弦长为 ,则双曲线的离心率等于 ( )
,则双曲线的离心率等于 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届上海市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
棱长为1的正方体 的8个顶点都在球面
的8个顶点都在球面 的表面上,
的表面上, 、
、 分别是棱
分别是棱 、
、 的中点,则直线
的中点,则直线 被球
被球 截得的线段长为________.
截得的线段长为________.
查看答案和解析>>
科目:高中数学 来源:2015届上海市高二下学期期中数学试卷(解析版) 题型:解答题
设 (
( 是正整数),利用赋值法解决下列问题:
是正整数),利用赋值法解决下列问题:
(1)求 ;
;
(2) 为偶数时,求
为偶数时,求 ;
;
(3) 是3的倍数时,求
是3的倍数时,求 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com