
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图(如图),解答下列问题:
分组 | 频数 | 频率 |
[50,60) | 4 | 0.08 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.20 |
[80,90) | 16 | 0.32 |
[90,100] | ||
合计 |
(1)填充频率分布表中的空格;
(2)不具体计算频率/组距,补全频率分布直方图.

【答案】(1)12,0.24,50,1; (2)见解析.
【解析】
试题分析:(1)由题根据频率分布表,知各组频率和为1,可推出[90,100],的频率并进而得出频数。再补全频率分布直方图。特别注意:纵坐标为频率除以组距。
(2)由(1)根据频率分布直方图算平均值的算法为,取各组的组中值乘以它的频率,再分别相加可得。
试题解析:(Ⅰ)抽取学生总数=![]()
50-(4+8+10+16)=12,![]()
所以,在区间[90,100]的频数为12,频率为0.24;
合计的频数为50,频率为1.00.
补全的频率分布直方图
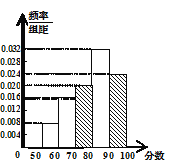
(Ⅱ)平均值为55×0.08+65×0.16+75×0.20+85×0.32+95×0.24=79.8.
所以,学生成绩的平均值为79.8.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=2, ![]() (n∈N*).
(n∈N*).
(1)证明数列 ![]() 是等比数列,并求数列{an}的通项公式;
是等比数列,并求数列{an}的通项公式;
(2)设 ![]() ,若数列{bn}的前n项和是Tn , 求证:
,若数列{bn}的前n项和是Tn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,证明:
两点,证明:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() 在棱
在棱![]() 上.
上.
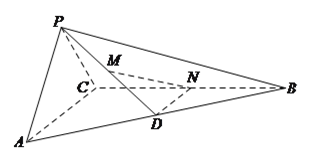
(![]() )当
)当![]() 为
为![]() 的中点时,证明:
的中点时,证明: ![]() 平面
平面![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )是否存在点
)是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,AB=1,BC=![]() ,AA1=2,E是侧棱BB1的中点.
,AA1=2,E是侧棱BB1的中点.
(1)求证:A1E⊥平面AED;
(2)求二面角A﹣A1D﹣E的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 在抛物线上.
在抛物线上.
(1)写出该抛物线的标准方程及其准线方程;
(2)过点![]() 作两条倾斜角互补的直线与抛物线分别交于不同的两点
作两条倾斜角互补的直线与抛物线分别交于不同的两点![]() ,求证:直线
,求证:直线![]() 的斜率是一个定值.
的斜率是一个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com