
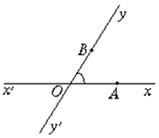
 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:分析 (1)设甲、乙两人t小时后的位置分别是P、Q,分情况讨论:当0<t≤$\frac{3}{4}$或t>$\frac{3}{4}$时,由余弦定理即可分别求PQ的值;
(2)由(1)可得PQ2=48(t-$\frac{1}{4}$)2+4,利用二次函数的性质即可求得t=$\frac{1}{4}$时两人的距离最短,最短距离为2km.
解答 解:(1)设甲、乙两人t小时后的位置分别是P、Q,
则AP=4t,BQ=4t,
(Ⅰ)当0≤t≤$\frac{3}{4}$时,
PQ=$\sqrt{(3-4t)^{2}+(1+4t)^{2}-2(3-4t)(1+4t)cos60°}$=$\sqrt{48{t}^{2}-24t+7}$.
(Ⅱ)当t>$\frac{3}{4}$时,
PQ=$\sqrt{(4t-3)^{2}+(1+4t)^{2}-2(4t-3)(1+4t)cos120°}$=$\sqrt{48{t}^{2}-24t+7}$,
综上(Ⅰ)、(Ⅱ)可知PQ═$\sqrt{48{t}^{2}-24t+7}$.
(2)∵PQ2=48(t-$\frac{1}{4}$)2+4,
∴当t=$\frac{1}{4}$时,(PQ)min=2,
即在第15分钟末,PQ最短,最短距离为2 km.
点评 本题主要考查了余弦定理在解三角形中的应用,正确分析实际问题中的边角关系是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | θ=$\frac{π}{4}$是f(x)=sin(x-2θ)的图象关于y轴对称的充分不必要条件 | |
| B. | |a|-|b|=|a-b|的充要条件是a与b的方向相同 | |
| C. | b=$\sqrt{ac}$是a,b,c三数成等比数列的充分不必要条件 | |
| D. | m=3是直线(m+3)x+my-2=0与mx-6y+5=0互相垂直的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
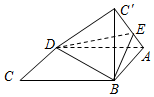 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com