
| A. | (-2,-1) | B. | (-1,0) | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
分析 根据导函数判断函数f(x)=ex+4x-3单调递增,运用零点判定定理,判定区间.
解答 解:∵函数f(x)=ex+4x-3
∴f′(x)=ex+4
当x>0时,f′(x)=ex+4>0
∴函数f(x)=ex+4x-3在(-∞,+∞)上为f(0)=e0-3=-2<0,
f($\frac{1}{2}$)=$\sqrt{e}$+2-3=$\sqrt{e}$-1=${e}^{\frac{1}{2}}$-e0>0,
∴f(0)•f($\frac{1}{2}$)<0,
∴函数f(x)=ex+4x-3的零点所在的区间为(0,$\frac{1}{2}$)
故选:C.
点评 本题考察了函数零点的判断方法,借助导数,函数值,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或2 | C. | $\frac{1}{2}$或2 | D. | $\frac{1}{2}或\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
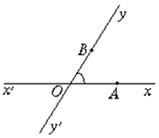 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com