
分析 (1)当a=1时,$f(x)=\frac{1}{2}{x^2}-2lnx-x$;对f(x)求导,利用导函数判断函数的单调性与求出函数的最值;
(2)f(x)的定义域为(0,+∞),${f^'}(x)=x-2\frac{a}{x}+a-2=\frac{{{x^2}+(a-2)x-2a}}{x}=\frac{(x-2)(x+a)}{x}$,对参数a分类讨论逐步判断原函数单调性即可;
(3)假设存在实数a,设0<x1<x2,$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>a$,即f(x2)-ax2>f(x1)-ax1,$g(x)=f(x)-ax=\frac{1}{2}{x^2}-2alnx+(a-2)x-ax=\frac{1}{2}{x^2}-2alnx-2x$;转化为:使g′(x)≥0在(0,+∞)恒成立,求a的范围.
解答 (1)当a=1时,$f(x)=\frac{1}{2}{x^2}-2lnx-x$.
则${f^'}(x)=x-\frac{2}{x}-1=\frac{{{x^2}-x-2}}{x}=\frac{(x+1)(x-2)}{x}$,x∈[1,e]
∴当x∈(1,2)时,f′(x)<0,当x∈(2,e)时,f′(x)>0,
∴f(x)在(1,2)上是减函数,在(2,e)上是增函数.
∴当x=2时,f(x)取得最小值,其最小值为f(2)=-2ln2.
又$f(1)=-\frac{1}{2}$,$f(e)=\frac{e^x}{2}-e-2$.$f(e)-f(1)=\frac{e^2}{2}-e-2+\frac{1}{2}=\frac{{{e^2}-2e-3}}{2}<0$,∴f(e)<f(1)
∴$f{(x)_{max}}=f(1)=-\frac{1}{2}$.
(2)f(x)的定义域为(0,+∞),${f^'}(x)=x-2\frac{a}{x}+a-2=\frac{{{x^2}+(a-2)x-2a}}{x}=\frac{(x-2)(x+a)}{x}$,
①当-2<a≤0时,f(x)在(0,-a)上是增函数,在(-a,2)上是减函数,在(2,+∞)上是增函数.
②当a=-2时,在(0,+∞)上是增函数.
③当a<-2时,则f(x)在(0,2)上是增函数,在(2,-a)上是减函数,在(-a,+∞)上是增函数.
(3)假设存在实数a,对任意的x1,x2∈(0,+∞),且x1≠x2,都有$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>a$恒成立,
不妨设0<x1<x2,若$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>a$,即f(x2)-ax2>f(x1)-ax1,
令$g(x)=f(x)-ax=\frac{1}{2}{x^2}-2alnx+(a-2)x-ax=\frac{1}{2}{x^2}-2alnx-2x$
只要g(x)在(0,+∞)为增函数${g^'}(x)=x-\frac{2a}{x}-2=\frac{{{x^2}-2x-2a}}{x}=\frac{{{{(x-1)}^2}-1-2a}}{x}$
要使g′(x)≥0在(0,+∞)恒成立,只需-1-2a≥0,$a≤-\frac{1}{2}$,
故存在$a∈(-∞,-\frac{1}{2}]$满足题意.
点评 本题主要考查了利用导函数判断函数单调性,分类讨论以及转化思想的应用,属综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
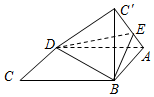 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| B. | “p∨q为真命题”的必要不充分条件是“p∧q为真命题” | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com