
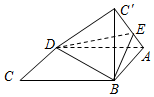
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则$\frac{AE}{EC′}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 取BD的中点O,连接AO,EO,C′O,推导出∠AOE=30°,∠EOC′=45°,∠OC′E=∠OAE,由正弦定理能求出$\frac{AE}{E{C}^{'}}$的值.
解答 解:取BD的中点O,连接AO,EO,C′O,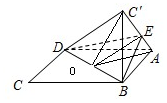
∵菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,
∴C′O⊥BD,AO⊥BD,OC′=OA,
∴BD⊥平面AOC′,
∴EO⊥BD,
∵二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,
∴∠AOE=30°,∠EOC′=45°,
∵OC′=OA,∴∠OC′E=∠OAE,
由正弦定理得$\frac{OE}{sin∠O{C}^{'}E}$=$\frac{E{C}^{'}}{sin∠EO{C}^{'}}$,
$\frac{OE}{sin∠OAE}=\frac{AE}{sin∠AOE}$,
∴$\frac{E{C}^{'}}{sin∠EO{C}^{'}}=\frac{AE}{sin∠AO{E}^{'}}$,
∴$\frac{AE}{E{C}^{'}}$=$\frac{sin30°}{sin45°}$=$\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}=\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查线段比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
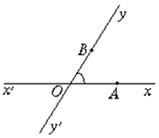 如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:
如图,有两条相交成60°角的直线xx′,yy′,交点是O,甲、乙分别在Ox,Oy上,起初甲离O点3km,乙离O点1km,后来两人同时用每小时4km的速度,甲沿xx′方向,乙沿y′y方向步行,问:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下:
为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定举行秋季校园足球联赛,为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,得到茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>3 | B. | a>-1 | C. | a≥-1 | D. | a≥3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com