
分析 (Ⅰ)求出当a=1时,f(x)的导数,判断符号,进而得到是否存在极值;
(Ⅱ)求出f9x)的导数,对a讨论,当a≤0时,当a≥1时,当0<a<1时,判断导数的符号,求出单调区间,即可得到.
解答 解:(Ⅰ)当a=1时,f(x)=x-$\frac{1}{x}$-2lnx,x>0,
f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=$\frac{(x-1)^{2}}{{x}^{2}}$≥0,
即有f(x)在(0,+∞)递增,函数f(x)不存在极值;
(Ⅱ)f(x)的定义域为(0,+∞),f′(x)=a(1+$\frac{1}{{x}^{2}}$)-$\frac{2}{x}$=$\frac{a{x}^{2}-2x+a}{{x}^{2}}$,
当a≤0时,f′(x)<0,f(x)在(0,+∞)递减;
当a>0时,x>0,f′(x)=0和方程ax2-2x+a=0由相同的实根,△=4-4a2,
①当0<a<1时,△>0,x1=$\frac{1-\sqrt{1-{a}^{2}}}{a}$,x2=$\frac{1+\sqrt{1-{a}^{2}}}{a}$,且x1<x2,
x∈(x1,x2)时,f′(x)<0,f(x)递减;x∈(0,x1)∪(x2,+∞)时,f′(x)>0,f(x)递增.
②当a≥1时,△≤0,f′(x)>0,f(x)递增.
综上可得,当a≤0时,f(x)的单调减区间为(0,+∞);
当0<a<1时,f(x)的减区间为($\frac{1-\sqrt{1-{a}^{2}}}{a}$,$\frac{1+\sqrt{1-{a}^{2}}}{a}$),
增区间为(0,$\frac{1-\sqrt{1-{a}^{2}}}{a}$),($\frac{1+\sqrt{1-{a}^{2}}}{a}$,+∞);
当a≥1时,f(x)的增区间为(0,+∞).
点评 本题考查导数的运用:求单调区间和极值,同时考查分类讨论的思想方法,注意化简和整理的运算能力的培养,属于中档题和易错题.


科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )
一个几何体的三视图如图所示,若该几何体的各顶点都在同一个球面上,则该几何体的侧视图的面积为 ( )| A. | 4+$\sqrt{2}$ | B. | 4+$\sqrt{3}$ | C. | 3+$\sqrt{2}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
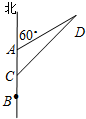 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com