
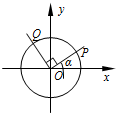
 在平面直角坐标系xOy中,设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转$\frac{π}{2}$后与单位圆交于点Q(x2,y2).记f(α)=y1+y2.
在平面直角坐标系xOy中,设锐角α的始边与x轴的非负半轴重合,终边与单位圆交于点P(x1,y1),将射线OP绕坐标原点O按逆时针方向旋转$\frac{π}{2}$后与单位圆交于点Q(x2,y2).记f(α)=y1+y2.分析 (1)根据三角函数的定义求出函数f(α)的表达式,即可求出处函数的值域;
(2)若f(C)=$\sqrt{2}$,则f(C)═$\sqrt{2}$sin(C+$\frac{π}{4}$)=,即可得到结论.
解答 解:(1)由三角函数定义知,y1=sinα,y2=sin(α+$\frac{π}{2}$)=cosα,
f(α)=y1+y2=cosα+sinα=$\sqrt{2}$sin(α+$\frac{π}{4}$),
∵角α为锐角,
∴$\frac{π}{4}$<α+$\frac{π}{4}$<$\frac{3π}{4}$,
∴<sin(α+$\frac{π}{4}$)≤1,
∴1<$\sqrt{2}$sin(α+$\frac{π}{4}$)≤$\sqrt{2}$,
则f(α)的取值范围是(1,$\sqrt{2}$];
(Ⅱ)若f(C)=$\sqrt{2}$,则f(C)═$\sqrt{2}$sin(C+$\frac{π}{4}$)=$\sqrt{2}$,
即sin(C+$\frac{π}{4}$)=1,
则C=$\frac{π}{4}$.
点评 本题主要考查三角函数的定义以及三角恒等变换的运用,根据条件求出函数的解析式是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-∞,-$\frac{1}{2}$)∪(2,+∞) | C. | (-$\frac{1}{2}$,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$=$\overrightarrow{b}$ | D. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
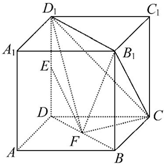 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为线段DD1,BD的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为线段DD1,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<2 } | B. | {x|0<x<2} | C. | {x|0≤x<l} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com