
���� ��1����2a=4��e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$�����a��c��ֵ������Բ�����ʿ�֪b2=a2-c2=1���������b�������ԲC�ķ��̣�
��2����ֱ�߷��̣����A��B���꣬��$\overrightarrow{FA}$•$\overrightarrow{FB}$=0�����������������ʾ�����b2=1+4k2����ֱ�ߴ�����Բ���̣��ɡ�=0��ֱ��l����Բ��1�����㣮
��� �⣺��1���������֪��2a=4��a=2��e=$\frac{c}{a}$=$\frac{{\sqrt{3}}}{2}$��
��c=$\sqrt{3}$��
b2=a2-c2��b=1��
����Բ����Ϊ��$\frac{{x}^{2}}{4}+{y}^{2}=1$��
��2����Ȼ��ֱ��l��б�ʴ��ڣ���ֱ�߷���Ϊl��y=kx+b��
��A��2��2k+b����B��-2��-2k+b����
��$\overrightarrow{FA}$•$\overrightarrow{FB}$=0����֪����2-$\sqrt{3}$��2k+b��•��-2-$\sqrt{3}$��-2k+b��=-1-4k2+b2=0��
��b2=1+4k2��
��ֱ��l��y=kx+b����Բ������x2+4��kx+b��2=4��
�ࣨ1+4k2��x2+8kbx+4b2-4=0��
��=64k2b2-4��1+4k2����4b2-4��
=64k2��1+4k2��-4��1+4k2����4+16k2-4��=0��
����ֱ�ߺ���Բǡ��һ�����㣮
���� ���⿼����Բ�ı����̣�ֱ������Բ��λ�ù�ϵ�������������������ʾ��������������������е��⣮


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-$\frac{1}{2}}$] | B�� | ��-�ޣ�-1] | C�� | [${\frac{1}{2}$��+�ޣ� | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=sin��$\frac{1}{3}$x+$\frac{��}{3}$����x��R | B�� | y=sin��3x+$\frac{��}{3}$����x��R | C�� | y=sin��3x+$\frac{��}{9}$����x��R | D�� | y=-sin3x��x��R |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��0�� | B�� | ��-$\frac{7}{2}$��+�ޣ� | C�� | ��-�ޣ�-$\frac{7}{2}$���ȣ�-1��+�ޣ� | D�� | ��-$\frac{7}{2}$��-1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
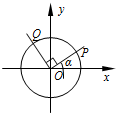 ��ƽ��ֱ������ϵxOy�У�����Ǧ���ʼ����x��ķǸ������غϣ��ձ��뵥λԲ���ڵ�P��x1��y1����������OP������ԭ��O����ʱ�뷽����ת$\frac{��}{2}$���뵥λԲ���ڵ�Q��x2��y2������f������=y1+y2��
��ƽ��ֱ������ϵxOy�У�����Ǧ���ʼ����x��ķǸ������غϣ��ձ��뵥λԲ���ڵ�P��x1��y1����������OP������ԭ��O����ʱ�뷽����ת$\frac{��}{2}$���뵥λԲ���ڵ�Q��x2��y2������f������=y1+y2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com