
 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这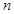 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时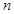 的最大值为3;当
的最大值为3;当 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时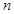 的最大值为4.则:
的最大值为4.则: 时,
时,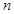 的最大值为________;(2)当
的最大值为________;(2)当 时,
时,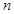 的最大值为________.
的最大值为________. 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源:不详 题型:单选题
| A.76 | B.80 | C.86 | D.92 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.各正三角形内一点 | B.各正三角形的某高线上的点 |
| C.各正三角形的中心 | D.各正三角形外的某点 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
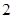 、
、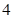 、
、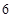 、
、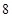 、
、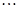 按表
按表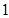 的方式进行排列,记
的方式进行排列,记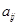 表示第
表示第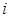 行和第
行和第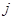 列的数,若
列的数,若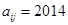 ,则
,则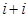 的值为( )
的值为( )| | 第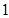 列 列 | 第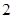 列 列 | 第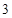 列 列 | 第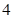 列 列 | 第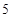 列 列 |
第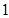 行 行 | | 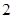 | 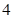 | 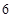 | 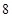 |
第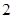 行 行 | 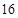 | 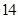 | 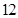 | 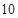 | |
第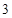 行 行 | | 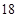 | 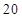 | 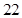 | 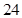 |
第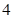 行 行 | 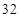 | 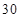 | 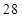 | 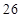 | |
第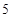 行 行 | | 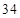 | 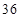 | 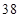 | 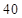 |
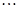 | 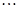 | 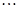 | 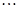 | 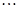 | 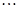 |
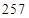 B.
B.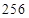 C.
C.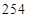 D.
D.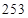
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (n≥2),每个数是它下一行左右相邻两数的和,如
(n≥2),每个数是它下一行左右相邻两数的和,如 =
= +
+ ,
, =
=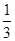 +
+ ,
,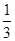 =
= +
+ ,则第10行第4个数(从左往右数)为( )
,则第10行第4个数(从左往右数)为( )
A.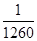 | B. |
C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com