
分析 综合法:利用作差法分析符号,推出结果即可.
分析法:利用分析法的证明步骤,找出不等式成立的充要条件即可.
解答 证明:综合法:3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)=(3a2-2b2)(a-b).
因为a≥b>0,所以a-b≥0,3a2-2b2>0,从而(3a2-2b2)(a-b)≥0,
所以3a3+2b3≥3a2b+2ab2.…(6分)
分析法:要证3a3+2b3≥3a2b+2ab2,只需证3a2(a-b)-2b2(a-b)≥0,
只需证(3a2-2b2)(a-b)≥0,∵a≥b>0.∴a-b≥0,
3a2-2b2>2a2-2b2≥0,
即:3a3+2b3≥3a2b+2ab2…(6分)
点评 本题考查不等式的证明,分析法以及综合法的应用,考查逻辑推理能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
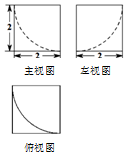
| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{8}{3}π$ | C. | 24-π | D. | 24+π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 1或$\frac{1}{2}$ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com