练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    定义在（0，
    π
    2
    ）上的函数y=2cosx与y=3tanx交点为P，则点P到x轴的距离为
     
    ．
    考点：余弦函数的图象,正切函数的图象
    专题：三角函数的求值,三角函数的图像与性质
    分析：首先建立方程组，根据sin2x+cos2x=1，进一步求得sinx的值，最后求得点P到x轴的距离．
    解答： 解：定义在（0，
    π
    2
    ）上的函数y=2cosx与y=3tanx交点为P
    则：
    y=2cosx
    y=3tanx

    2cosx=3tanx=3
    sinx
    cosx

    2sin2x+3sinx-2=0
    解得：sinx=
    1
    2
    或-2（负值舍去）
    所以：sinx=
    1
    2

    cosx=
    		3
    2

    则：点P到x轴的距离为：
    		3

    故答案为：
    		3
    点评：本题考查的知识要点：解方程组问题合同叫三角函数的恒等变形，属于基础题型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列各组函数中，表示同一个函数的是（　　）
    A、f（x）=
    		x2
    ，g（x）=x
    B、f（x）=log22x，g（x）=
    3x3
    C、f（x）=x，g（x）=
    x2
    x
    D、f（x）=lnx2，g（x）=2lnx

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线C：y2=4x，直线l过定点M（a，0），a＞0且与抛物线交于A、B两点，O为坐标原点，若∠AOB为锐角，则实数a的取值范围是（　　）
    A、0＜a＜4B、a＞4
    C、a≥2D、0＜a＜2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x3+ax2+bx+c在点M（1，f（1））处的切线方程为3x-y+1=0，且在x=
    2
    3
    处有极值．
    （1）求函数y=f（x）的解析式；  
    （2）求函数y=f（x）的极大值与极小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设点P在双曲线
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的右支上，双曲线两焦点F1、F2，|PF1|=4|PF2|，求双曲线离心率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

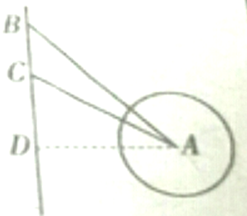    某学校组织同学们参加红色七日游--还上夏令营活动，如图，海中小岛A周围20海里内有暗礁，夏令营的船只正向南航行，在B处测得小岛A在船的南偏东30°；航行30海里后，在C处测得小岛A在船的南偏东60°，如果此船不改变航向，继续向南航行，有无触礁危险？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设
    a
    ，
    b
    ，
    c
    为单位向量，
    a
    ，
    b
    的夹角为60°，则（
    a
    +
    b
    ）•
    c
    的最大值为（　　）
    A、
    		3
    B、
    3
    2
    C、3
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）上存在点P使
    PF1
    •
    PF2
    ＜0，则离心率e∈（　　）
    A、（0，
    		2
    2
    ）
    B、（0，
    		2
    2
    ]
    C、（
    		2
    2
    ，1）
    D、（
    		2
    2
    ，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2sin（ωx+
    π
    6
    ）（ω＞0），y=f（x）的图象与直线y=2的两个相邻交点的距离的最小值等于
    π
    3
    ，则f（x）的单调递增区间是
     
    ．

    查看答案和解析>>

    同步练习册答案