暑假作业暑假快乐练西安出版社系列答案科目：高中数学 来源：2017届广州省惠州市高三第一次调研文科数学试卷（解析版） 题型：解答题
为了迎接第二届国际互联网大会，组委会对报名参加服务的1500名志愿者进行互联网知识测试，从这1500名志愿者中采用随机抽样的方法抽取15人，所得成绩如下：57，63，65，68，72，77，78，78，79，80，83，85，88，90，95.
（Ⅰ）作出抽取的15人的测试成绩的茎叶图，以频率为概率，估计这1500志愿者中成绩不低于90分的人数；
（Ⅱ）从抽取的成绩不低于80分的志愿者中，随机选3名参加某项活动，求选取的3人中恰有一人成绩不低于90分的概率.
查看答案和解析>>
科目：高中数学 来源：2017届广州省惠州市高三第一次调研文科数学试卷（解析版） 题型：选择题
已知三棱锥
的底面是以
为斜边的等腰直角三角形,
则三棱锥的外接球的球心到平面
的距离是（ ）
（A）
（B）1 （C）
（D）
查看答案和解析>>
科目：高中数学 来源：2015-2016学年黑龙江鹤岗一中高二下期末理科数学试卷（解析版） 题型：填空题
已知
为定义在
上的偶函数，当
时，有
，且当
时，
，给出下列命题：
①
；
②函数在定义域上是周期为2的函数；
③直线
与函数的图象有2个交点；
④函数的值域为
．
其中正确的是 ．
查看答案和解析>>
科目：高中数学 来源：2016届北京市大兴区高三4月统一练习文科数学试卷（解析版） 题型：解答题
已知函数
，
．
（1）若曲线
在点(0，f(0))处的切线方程为y=-4x-2，求a的值；
（2）求函数
的单调区间；
（3）当a=1时，对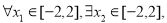
使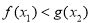
，求实数c的取值范围.
查看答案和解析>>
科目：高中数学 来源：2015-2016学年广东实验中学等高二下期末理科数学试卷（解析版） 题型：解答题
已知梯形
所在平面垂直于平面
于
，
∥
， 
，
，
．
（1）求证：
；
（2）求平面
与平面
所成的锐二面角的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的各项为正数，且
，则
（ ）
（B）
（C）
（D）
，则函数
的大致图像为（ ）
，
，则
.
，
，则
（ ）
（B）
（C）
（D）