营养学家指出，高中学生良好的日常饮食应该至少提供0. 075kg的碳水化合物，0.06kg的蛋白质，0.06kg的脂肪。1kg食物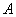
含有0.105kg碳水化合物，0.07kg蛋白质，0.14kg脂肪，花费
元；而1kg食物
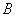含有0.105kg碳水化合物，0.14kg蛋白质，0.07kg脂肪，花费
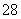元。为了满足营养专家指出的 日常饮食要求，同时使花费最低，需要同时食用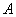食物和食物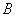多少kg？
科目：高中数学 来源： 题型：
定义在实数集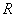
上的函数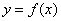
的图象是连续不断的，若对任意实数
，存在实数
使得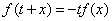
恒成立，则称
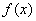是一个“关于的函数”，给出下列“关于的函数”的结论：
①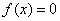
是常数函数中唯一一个“关于的函数”；②“关于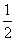
的函数”至少有一个零点；③
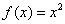是一个“关于的函数”．
其中正确结论的个数是
A．0 B．1 C．2 D．3
查看答案和解析>>
科目：高中数学 来源： 题型：
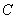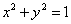已知曲线
：
，将曲线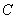上的点按坐标变换
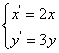得到曲线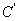
；以直角坐标系原点为极点，
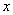轴的正半轴为极轴建立极坐标系，直线
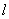的极坐标系方程是
。
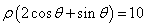⑴写出曲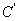线和直线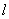的普通方程；
⑵求曲线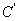上的点
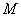到直线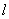距离的最大值及此时点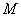的坐标。
查看答案和解析>>
科目：高中数学 来源： 题型：
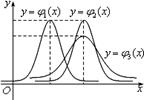
已知三个正态分布密度函数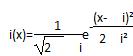
(xR,i=1,2,3)的图象如图所示,则 ( )
A.1<2=3, 1=2>3 B.1>2=3, 1=2<3
C.1=2<3, 1<2=3 D.1<2=3, 1=2<3
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面直角坐标系中，设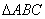
的顶点分别为
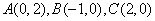，圆
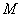是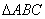的外接圆，直线
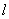的方程是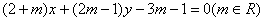
（1）求圆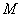的方程；
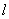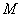（2）证明：直线与圆相交；
（3）若直线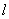被圆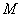截得的弦长为3,求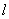的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
解：设每天食用
食物，
食物，总成本为
。则
------------------4分
，
--------------10分
，食物
，能够满足日常饮食要求，又使花费最低，最低成本21元。--------------12分
的焦点为F，准线为
，P是
，则
内，过点
的最长弦和最短弦分别为
和
，则四边形
的面积为（ ）
B．
C．
． D．
(
﹥
,
﹥
，则其渐近线方程为 。