
已知曲线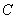 :
: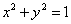 ,将曲线
,将曲线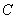 上的点按坐标变换
上的点按坐标变换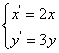 得到曲线
得到曲线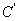 ;以直角坐标系原点为极点,
;以直角坐标系原点为极点,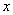 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线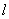 的极坐标系方程是
的极坐标系方程是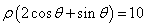 。
。
⑴写出曲线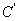 和直线
和直线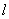 的普通方程;
的普通方程;
⑵求曲线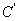 上的点
上的点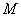 到直线
到直线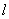 距离的最大值及此时点
距离的最大值及此时点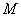 的坐标。
的坐标。
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
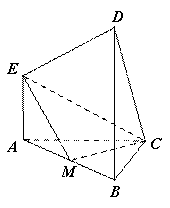
在如图所示的多面体中,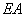 ⊥平面
⊥平面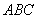 ,
,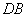 ⊥平面ABC,
⊥平面ABC,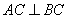 ,且
,且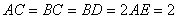 ,
,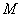 是
是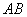 的中点.
的中点.
(Ⅰ)求证: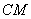 ⊥
⊥ ;
;
(Ⅱ)求平面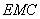 与平面
与平面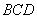 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(Ⅲ)在棱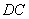 上是否存在一点
上是否存在一点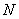 ,使得直线
,使得直线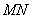 与平面
与平面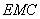 所成的角为
所成的角为 .若存在,指出点
.若存在,指出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
某运输公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆 型卡车和8辆
型卡车和8辆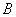 型卡车.又已知
型卡车.又已知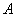 型卡车每天每辆的运载量为30吨,成本费为0.9千元;
型卡车每天每辆的运载量为30吨,成本费为0.9千元;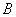 型卡车每天每辆的运载量为40吨,成本费为1千元,则该公司所花的最小成本费是 .
型卡车每天每辆的运载量为40吨,成本费为1千元,则该公司所花的最小成本费是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
营养学家指出,高中学生良好的日常饮食应该至少提供0. 075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪。1kg食物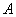 含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费
含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费 元;而1kg食物
元;而1kg食物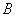 含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费
含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费 元。为了满足营养专家指出的 日常饮食要求,同时使花费最低,需要同时食用食物
元。为了满足营养专家指出的 日常饮食要求,同时使花费最低,需要同时食用食物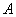 和食物
和食物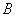 多少kg?
多少kg?
查看答案和解析>>
科目:高中数学 来源: 题型:
为了考查两个变量x和y之间的线性关系,甲、乙两位同学各自独立做了8次和10次试验,并且利用线性回归方法,求得回归直线分别为l1,l2,已知两人得到的试验数据中,变量x和y的数据的平均值都分别相等,则下列说法正确的是 ( )
A.直线l1和l2必定重合 B.必有l1//l2
C.直线l1和l2不一定相交 D.直线l1和l2一定有公共点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com