
分析 (1)f(x)=2即ex-$\frac{1}{{e}^{x}}$=2,先解ex,再解x值,注意ex>0;
(2)不等式f(2t)-mf(t)≥0恒成立,通过整理变形转化为m≤et+$\frac{1}{{e}^{t}}$恒成立,分离参数m后转化为求函数最值问题解决.
解答 解:(1)若x≤0,则f(x)=ex-ex=0,
f(x)=2即ex-$\frac{1}{{e}^{x}}$=2,(x>0),
得e2x-2•ex-1=0,
∴ex=1-$\sqrt{2}$(舍去)或ex=1+$\sqrt{2}$,
∴x=ln(1+$\sqrt{2}$);
(2)由x>0可得f(x)=ex-$\frac{1}{{e}^{x}}$,
不等式f(2t)-mf(t)≥0对t∈[1,2]恒成立,即为
e2t-$\frac{1}{{e}^{2t}}$-m(et-$\frac{1}{{e}^{t}}$)≥0,
∵t∈[1,2],∴e2t>$\frac{1}{{e}^{2t}}$,et>$\frac{1}{{e}^{t}}$,
∴m≤et+$\frac{1}{{e}^{t}}$恒成立,
由于t∈[1,2],则et∈[e,e2],
即有et+$\frac{1}{{e}^{t}}$的最小值为e+$\frac{1}{e}$,
∴m≤e+$\frac{1}{e}$,
因此m的最大值为e+$\frac{1}{e}$.
点评 本题考查函数恒成立问题及指数方程的求解,考查学生的分析问题解决问题的能力,恒成立问题往往转化为求函数最值问题解决,或分离参数后再求函数最值.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
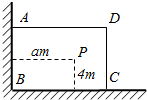 如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.
如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com