
 在△ABC中,已知∠BAC=α,AB=c,AC=b,如图建立直角坐标系,利用两点间的距离公式计算BC2,并由此证明余弦定理.
在△ABC中,已知∠BAC=α,AB=c,AC=b,如图建立直角坐标系,利用两点间的距离公式计算BC2,并由此证明余弦定理.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| cosB |
| sinBcosC |
| 1 |
| 2sinA-sinC |
查看答案和解析>>
科目:高中数学 来源: 题型:
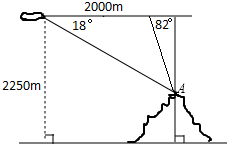 如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为
如图,一只气球在2250m的高空水平飞行,气球上的工作人员测得前方一座山顶上A点处的俯角为18°,当气球向前飞行了2000m后,又测得前方A点处的俯角为82°,则山的高度为查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
A、32
| ||||
B、32
| ||||
C、32
| ||||
D、64
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com