
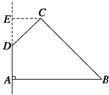
 如图所示,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
如图所示,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.分析 画出四边形ABCD绕AD旋转一周所成几何体,然后求出圆台的底面积、圆台的侧面积及圆锥的侧面积作和得答案;由圆台的体积减去圆锥的体积求得几何体的体积.
解答 解:如图,∵∠ADC=135°,∴∠CDE=45°,又CD=2$\sqrt{2}$,
∴DE=CE=2,又AB=5,AD=2,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}=5$.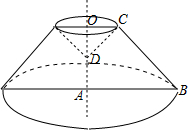
则圆台上底面半径r1=2,下底面半径r2=5,高h=4,母线长l=5,圆锥底面半径r1=2,高h′=2.
∴S表面=S圆台底面+S圆台侧面+S圆锥侧面=π×52+π×(2+5)×5+π×2×2$\sqrt{2}$
=(4$\sqrt{2}$+60)π;
V=V圆台-V圆锥=$\frac{1}{3}$π(${{r}_{1}}^{2}$+r1r2+${{r}_{2}}^{2}$)h-$\frac{1}{3}$π${{r}_{1}}^{2}$h′=$\frac{1}{3}$π(25+10+4)×4-$\frac{1}{3}$π×4×2=$\frac{148}{3}$π.
点评 本题考查圆锥、圆台的体积的求法,明确四边形ABCD绕直线AD旋转所得图形是解答该题的关键,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 4 | C. | $2\sqrt{6}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com