
设函数f(x)=lnx+ln(2-x)+ax(a>0).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)在(0,1]上 的最大值为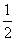 ,求a的值.
,求a的值.
科目:高中数学 来源: 题型:
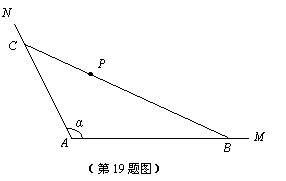
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,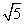 km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
航空母舰“辽宁舰”将进行一次编队配置科学实验,要求2艘攻击型核潜艇一前一后,2艘驱逐舰和2艘护卫舰分列左、右,同侧不能都是同种舰艇,则舰艇分配方案的方法数为________.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com