
分析 (1)利用向量坐标运算性质即可得出.
(2)利用向量夹角公式、数量积运算性质即可得出.
解答 解:(1)$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$=(4,4)-(1,1)=(3,3).
(2)$\overrightarrow{AB}$=(2,0),$\overrightarrow{AC}$=(3,3).
∴$\overrightarrow{AB}•\overrightarrow{AC}$=6,
$cos<\overrightarrow{AB},\overrightarrow{AC}>$=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{6}{2×3\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
可得∠BAC=$\frac{π}{4}$.
点评 本题考查了向量坐标运算性质、向量夹角公式、数量积运算性质,考查了推理能力与计算能力,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | (1,2] | C. | [1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
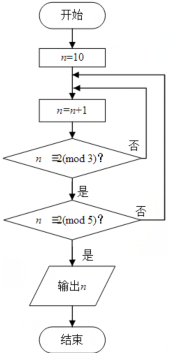 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )| A. | 44,45,56 | B. | 44,43,57 | C. | 44,43,56 | D. | 45,43,57 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com