
 如图,在直三棱柱ABC-A1B1C1中,底面是正三角形,点D是A1B1中点,AC=2,CC1=$\sqrt{2}$.
如图,在直三棱柱ABC-A1B1C1中,底面是正三角形,点D是A1B1中点,AC=2,CC1=$\sqrt{2}$.分析 (Ⅰ)利用${V_{C-BD{C_1}}}={V_{D-BC{C_1}}}$,求三棱锥C-BDC1的体积;
(Ⅱ)取C1B1的中点E,连接A1E,CE.通过证明$BC_1^{\;}⊥$面A1CE,证明:A1C⊥BC1.
解答 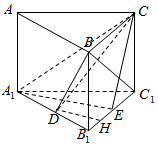 (Ⅰ)解:过D作DH⊥C1B1,直三棱柱中C1B1⊥面A1B1C1,∴C1B1⊥DH,∴DH⊥面BCC1,
(Ⅰ)解:过D作DH⊥C1B1,直三棱柱中C1B1⊥面A1B1C1,∴C1B1⊥DH,∴DH⊥面BCC1,
∴DH是高,DH=$\frac{{\sqrt{3}}}{2}$,…(3分)
∵${S_{△BC{C_1}}}=\frac{1}{2}×2×\sqrt{2}=\sqrt{2}$,
∴${V_{C-BD{C_1}}}={V_{D-BC{C_1}}}=\frac{1}{3}×\frac{{\sqrt{3}}}{2}×\sqrt{2}=\frac{{\sqrt{6}}}{6}$•…(6分)
(Ⅱ)证明:取C1B1的中点E,连接A1E,CE
∵底面是正三角形,∴A1E⊥B1C1•…(8分)
矩形C1B1BC中,Rt△C1CE中,${C_1}C=\sqrt{2},{C_1}E=1$,
Rt△BCC1中,$BC=2,C{C_1}=\sqrt{2}$,∴$\frac{{{C_1}C}}{BC}=\frac{{{C_1}E}}{{C{C_1}}}$,
∴△C1CE∽△BCC1,∴∠C1BC=∠EC1C,
∵$∠{C_1}BC+∠B{C_1}C={90^0}$,∴$∠EC{C_1}+∠B{C_1}C={90^0}$,∴CE⊥BC1•…(10分)
∴$BC_1^{\;}⊥$面A1CE,∴A1C⊥BC1•…(12分)
点评 本题考查线面垂直的判定定理与性质、空间几何体的体积,考查学生分析解决问题的能力,属于中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-5,-2] | B. | (-5,-2) | C. | (2,5) | D. | [2,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
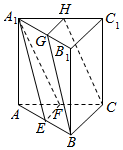 如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
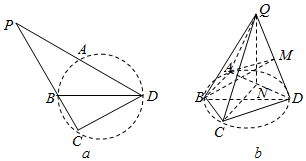 如图(a)已知线段BD=4,A,C关于BD对称,以BD为直径作圆,经过A,C两点,BA=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点Q位置,得到图(b)所示空间图形,其中Q在平面ABCD内的射影恰为线段AD中点N,QD中点为M.
如图(a)已知线段BD=4,A,C关于BD对称,以BD为直径作圆,经过A,C两点,BA=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点Q位置,得到图(b)所示空间图形,其中Q在平面ABCD内的射影恰为线段AD中点N,QD中点为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
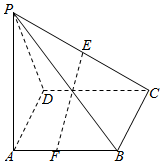 如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点
如图,四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E、F分别为PC、AB的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com