
【题目】已知函数f(x)=ex+ax+b(a≠0,b≠0).
(1)若函数f(x)的图象在点(0,f(0))处的切线方程为y=2,求f(x)在区间[﹣2,1]上的最值;
(2)若a=﹣b,试讨论函数f(x)在区间(1,+∞)上零点的个数.
【答案】
(1)解:∵f(x)=ex+ax+b,∴f′(x)=ex+a,
∴f′(0)=1+a,
∵函数f(x)的图象在点(0,f(0))处的切线方程为y=2,
∴a=﹣1.
∵x=0,f(0)=2,
∴1+b=2,
∴b=1,
∴f(x)=ex﹣x+1,
∴f′(x)=ex﹣1,
当x<0时,有f′(x)<0,f(x)递减,
当x>0时,有f′(x)>0,f(x)递增.
则x=0处f(x)取得极小值,也为最小值,且为2,
又f(﹣2)=e﹣2+3,f(1)=e,f(2)>f(1),
即有f(﹣2)为最大值e﹣2+3;
(2)解:若a=﹣b,f(x)=ex+ax﹣a=0,x>1,﹣a= ![]() ,
,
令g(x)= ![]() ,则g′(x)=
,则g′(x)= ![]() ,
,
当x>2时,g′(x)>0,g(x)递增,
当x<1和1<x<2时,g′(x)<0,g(x)递减.
即有x=2处g(x)取得极小值,为e2,
∴﹣a<e2,即a>﹣e2,函数f(x)在区间(1,+∞)上零点的个数为0;
﹣a=e2,即a=﹣e2,函数f(x)在区间(1,+∞)上零点的个数为1;
﹣a>e2,即a<﹣e2,函数f(x)在区间(1,+∞)上零点的个数为2.
【解析】(1)求出导数,利用函数f(x)的图象在点(0,f(0))处的切线方程为y=2,解得a=﹣1,b=1,求得极小值2,也为最小值,再求f(﹣2)和f(1),比较即可得到最大值;(2)若a=﹣b,f(x)=ex+ax﹣a=0,x>1,﹣a= ![]() ,g(x)=
,g(x)= ![]() ,求出导数,求得单调区间和极值,即可讨论函数f(x)在区间(1,+∞)上零点的个数.
,求出导数,求得单调区间和极值,即可讨论函数f(x)在区间(1,+∞)上零点的个数.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a、b为常数),且f(1)=
(a、b为常数),且f(1)= ![]() ,f(0)=0.
,f(0)=0.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在定义域上的奇偶性,并证明;
(3)对于任意的x∈[0,2],f(x)(2x+1)<m4x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:分子为1且分母为正整数的分数叫做单位分数,我们可以把1拆分成多个不同的单位分数之和.例如:1= ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,…,依此拆分法可得1=
,…,依此拆分法可得1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,其中m,n∈N* , 则m﹣n=( )
,其中m,n∈N* , 则m﹣n=( )
A.﹣2
B.﹣4
C.﹣6
D.﹣8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,符号[x]表示不超过x的最大整数,如[2.2]=2,[﹣3.5]=﹣4,设数列{an}的通项公式为an=[log21]+[log22]+[log23]+…[log2(2n﹣1)].
(1)求a1a2a3的值;
(2)是否存在实数a,使得an=(n﹣2)2n+a(n∈N*),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(﹣1,4)及圆C:(x﹣2)2+(y﹣3)2=1.则下列判断正确的序号为 .
①点P在圆C内部;
②过点P做直线l,若l将圆C平分,则l的方程为x+3y﹣11=0;
③过点P做直线l与圆C相切,则l的方程为y﹣4=0或3x+4y﹣13=0;
④一束光线从点P出发,经x轴反射到圆C上的最短路程为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣kx,x∈R(e是自然对数的底数).
(1)若k∈R,求函数f(x)的单调区间;
(2)若k>0,讨论函数f(x)在(﹣∞,4]上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() (α为参数)与曲线C2:ρ=4sinθ
(α为参数)与曲线C2:ρ=4sinθ
(1)写出曲线C1的普通方程和曲线C2的直角坐标方程;
(2)求曲线C1和C2公共弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0)的部分图象如图所示,下面结论正确的个数是( )
①函数f(x)的最小正周期是2π
②函数f(x)的图象可由函数g(x)=sin2x的图象向左平移 ![]() 个单位长度得到
个单位长度得到
③函数f(x)的图象关于直线x= ![]() 对称
对称
④函数f(x)在区间[ ![]() ]上是增函数.
]上是增函数.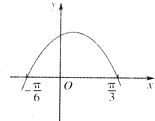
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com