
【题目】集合A= ![]() ,若BA求m的取值范围.
,若BA求m的取值范围.
【答案】解:集合A中的不等式组得:集合A={x|﹣2<x<5},
进而分2种情况讨论:
①B=Ф,此时符合BA,
若m+1>2m﹣1,解可得m<2,
此时,m<2;
②B≠Ф,即m+1≤2m﹣1时,
要使BA,
则 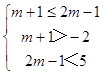 ,
,
解得:2≤m<3,
综合①②得m的取值范围是{m|m<3}
【解析】根据题意,解集合A中的不等式组,可得集合A={x|﹣2<x<5},进而对m分2种情况讨论:①B=Ф,即m+1>2m﹣1时,解可得m的范围,②B≠Ф,即m+1≤2m﹣1时,要使BA,必有则 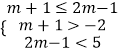 ,解可得m的取值范围,综合2种情况即可得答案.
,解可得m的取值范围,综合2种情况即可得答案.
【考点精析】解答此题的关键在于理解子集与真子集的相关知识,掌握任何一个集合是它本身的子集;n个元素的子集有2n个,n个元素的真子集有2n -1个,n个元素的非空真子集有2n-2个.


科目:高中数学 来源: 题型:
【题目】二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2 , 三维测度(体积)V= ![]() πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
πr3;四维空间中“超球”的三维测度V=8πr3 , 则猜想其四维测度W= .
查看答案和解析>>
科目:高中数学 来源: 题型:
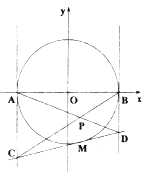
【题目】已知圆![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,圆
的任意一点,圆![]() 在点
在点![]() 处的切线与圆
处的切线与圆![]() 在点
在点![]() 处的切线分别交于
处的切线分别交于![]() ,直线
,直线![]() 和
和![]() 交于点
交于点![]() ,设
,设![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴正半轴交点为
轴正半轴交点为![]() ,则曲线
,则曲线![]() 是否存在直角顶点为
是否存在直角顶点为![]() 的内接等腰直角三角形
的内接等腰直角三角形![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 的两条直角边所在直线的方程,若不存在,请说明理由.
的两条直角边所在直线的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,定义椭圆的“伴随圆”方程为
,定义椭圆的“伴随圆”方程为![]() ;若抛物线
;若抛物线![]() 的焦点与椭圆C的一个短轴端点重合,且椭圆C的离心率为
的焦点与椭圆C的一个短轴端点重合,且椭圆C的离心率为![]() .
.
(1)求椭圆C的方程和“伴随圆”E的方程;
(2)过“伴随圆”E上任意一点P作椭圆C的两条切线PA,PB,A,B为切点,延长PA与“伴随圆”E交于点Q,O为坐标原点.
(i)证明:PA⊥PB;
(ii)若直线OP,OQ的斜率存在,设其分别为![]() ,试判断
,试判断![]() 是否为定值,若是, 求出该值;若不是,请说明理由.
是否为定值,若是, 求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )与直线
)与直线![]() :
: ![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, ![]() ,
, ![]() 中有三个点在椭圆
中有三个点在椭圆![]() 上,剩余一个点在直线
上,剩余一个点在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() ,
, ![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax+b(a≠0,b≠0).
(1)若函数f(x)的图象在点(0,f(0))处的切线方程为y=2,求f(x)在区间[﹣2,1]上的最值;
(2)若a=﹣b,试讨论函数f(x)在区间(1,+∞)上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣ ![]() ,g(x)=
,g(x)= ![]() sin2x.
sin2x.
(1)求函数f(x)与g(x)图象交点的横坐标;
(2)若函数φ(x)= ![]() ﹣f(x)﹣g(x),将函数φ(x)图象上的点纵坐标不变,横坐标扩大为原来的4倍,再将所得函数图象向右平移
﹣f(x)﹣g(x),将函数φ(x)图象上的点纵坐标不变,横坐标扩大为原来的4倍,再将所得函数图象向右平移 ![]() 个单位,得到函数h(x),求h(x)的单调递增区间.
个单位,得到函数h(x),求h(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
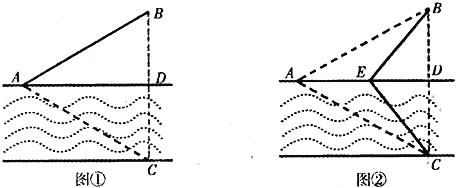
【题目】如图①,一条宽为1km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(1)已知村庄A与B原来铺设有旧电缆,但旧电缆需要改造,改造费用是0.5万元/km.现决定利用此段旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值;
(2)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ(0≤θ≤![]() ),试用θ表示出总施工费用y (万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y (万元)的解析式,并求y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com