
| A. | $\sqrt{37}$-3 | B. | $\sqrt{37}$+3 | C. | $\sqrt{10}$ | D. | $\sqrt{82}$ |
分析 设动点的坐标为P(x,y),求得2$\overrightarrow{AP}$+$\overrightarrow{BP}$ 的坐标,可得|2$\overrightarrow{AP}$+$\overrightarrow{BP}$|=$\sqrt{36x-6y-26}$.结合(x-2)2+y2=1,则令x=2+cosθ,y=sinθ,化简36x-6y-26为 6$\sqrt{37}$cos(θ+φ)+46,利用余弦函数的值域求得它的最大值,可得结论.
解答 解:设动点的坐标为P(x,y),则$\overrightarrow{AP}$=(x,y-1),$\overrightarrow{BP}$=(x,y+1),$\overrightarrow{PC}$=(1-x,-y).
∵$\overrightarrow{AP}$•$\overrightarrow{BP}$=2 ${|\overrightarrow{PC}|}^{2}$,∴x2+y2-1=2[(x-1)2+y2],
∴x2+y2-4x+3=0,即:(x-2)2+y2=1.
∵2$\overrightarrow{AP}$+$\overrightarrow{BP}$=2(x,y-1)+(x,y+1)=(3x,3y-1),
∴|2$\overrightarrow{AP}$+$\overrightarrow{BP}$|=$\sqrt{{9x}^{2}+{9y}^{2}-6y+1}$=$\sqrt{36x-6y-26}$.
又∵(x-2)2+y2=1,则令x=2+cosθ,y=sinθ,
于是有36x-6y-26=36cosθ-6sinθ+46
=6$\sqrt{37}$cos(θ+φ)+46∈[46-6$\sqrt{37}$,46+6$\sqrt{37}$],
故|2$\overrightarrow{AP}$+$\overrightarrow{BP}$|的最大值为 $\sqrt{46+6\sqrt{37}}$=$\sqrt{37}$+3,
故选:B.
点评 本题主要考查两个向量的坐标形式的运算,两个向量的数量积的运算,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 焦距相等 | B. | 离心率相等 | C. | 焦点相同 | D. | 有相等的长、短轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
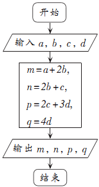
| A. | 4,6,1,7 | B. | 7,6,1,4 | C. | 1,6,4,7 | D. | 6,4,1,7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
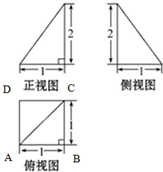 已知一四棱锥P-ABCD的三视图如图.
已知一四棱锥P-ABCD的三视图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 240 | B. | 360 | C. | 480 | D. | 720 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com