
 如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为6海里,在A处看灯塔C在货轮的北偏西30°,距离为4海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
如图,某货轮在A处看灯塔B在货轮的北偏东75°,距离为6海里,在A处看灯塔C在货轮的北偏西30°,距离为4海里,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:分析 (1)在△ABD中使用正弦定理解出;
(2)在△ACD中使用余弦定理解出.
解答 解:(1)在△ABD中,AB=6,∠ADB=60°,∠BAD=75°,∴B=45°,
由正弦定理得AD=$\frac{AB•sin45°}{sin60°}$=2$\sqrt{6}$,∴A处与D处的距离为4$\sqrt{6}$nmile.
(2)在△ADC中,AC=4,AD=2$\sqrt{6}$,∠CAD=30°,
∴CD2=AD2+AC2-2AD•AC•cos30°.解得CD=2$\sqrt{10-6\sqrt{2}}$.
∴灯塔C与D处的距离为2$\sqrt{10-6\sqrt{2}}$nmile.
点评 本题考查了解三角形的应用,构造合适的三角形是关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | -C73C4343-47 | B. | -C72C4243+47 | C. | -47 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=-x+1.
已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=-x+1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
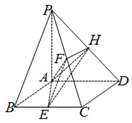 如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F、H分别是BC、PC、PD的中点.
如图,已知四棱锥P-ABCD的底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F、H分别是BC、PC、PD的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com