练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．一条光线从A（-$\frac{1}{2}$，0）处射到点B（0，1）后被y轴反射，则反射光线所在直线的方程为（　　）
    A．2x-y-1=0B．2x+y-1=0C．x-2y-1=0D．x+2y+1=0

    分析 由反射定律可得点A（-$\frac{1}{2}$，0）关于y轴的对称点A′（$\frac{1}{2}$，0）在反射光线所在的直线上，再根据点b（0，1）也在反射光线所在的直线上，用两点式求得反射光线所在的直线方程．

    解答 解：由反射定律可得点点A（-$\frac{1}{2}$，0）关于y轴的对称点A′（$\frac{1}{2}$，0）在反射光线所在的直线上，
    再根据点B（0，1）也在反射光线所在的直线上，
    用两点式求得反射光线所在的直线方程为$\frac{y-1}{0-1}$=$\frac{x-0}{\frac{1}{2}-0}$，即2x+y-1=0，
    故选：B．

    点评 本题主要考查求一个点关于直线的对称点的坐标，用两点式求直线的方程，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．关于x的不等式mx2-ax-1＞0（m＞0）的解集可能是（　　）
    A．{x|x＜-1或x＞$\frac{1}{4}$}B．RC．{x|-$\frac{1}{3}$＜x＜$\frac{3}{2}$}D．∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．设函数f（x）=|3x-1|+ax+3，a∈R．
    （1）若a=1，解不等式f（x）≤4；
    （2）若函数f（x）有最小值，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知曲线C：y=$\sqrt{4-{x^2}}$（-2≤x≤0）与函数f（x）=loga（-x）及函数g（x）=a-x（a＞1）的图象分别交于A（x1，y1），B（x2，y2）两点，则x12+x22的值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设集合A={x|-2≤x≤5}，B={x|m+1≤x≤2m-1}，
    （1）若m=4，求A∪B；
    （2）若B⊆A，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{10}）^{x}，x≤10}\\{-lg（x+2），x＞10}\end{array}\right.$，若f（8-m2）＜f（2m），则实数m的取值范围是（　　）
    A．（-4，2）B．（-4，1）C．（-2，4）D．（-∞，-4）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

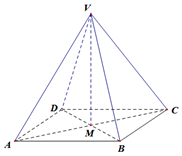    3．如图，已知正四棱锥V-ABCD中，AC与BD交于点M，VM是棱锥的高，若AC=6cm，VC=5cm．
    （1）求正四棱锥V-ABCD的体积；
    （2）求直线VD与底面ABCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知集合A={x|x≥1}，B={x|x＞2a+1}，若A∩（∁RB）=∅，则实数a的取值范围是（　　）
    A．（1，+∞）B．（0，+∞）C．（-∞，1）D．（-∞，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

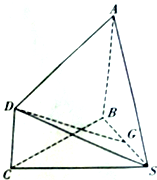    19．如图，在几何体S-ABCD中，AB⊥平面SBC，CD⊥平面SBC，SB⊥SC，AB=SB=SC=2CD=2，G是线段BS的中点．
    （1）求GD与平面SCD所成角的正弦值；
    （2）求平面SAD与平面SBC所成锐二面角的余弦值．

    查看答案和解析>>

    同步练习册答案