
【题目】给出下列五个命题:
①当![]() 时,有
时,有![]() ;
;
②若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ;
;
④函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
⑤当![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
的取值范围为![]() .
.
其中正确命题的序号为___________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某几何体的三视图和直观图如图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
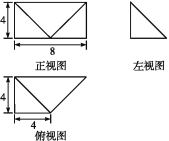
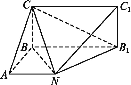
(1)证明:平面BCN⊥平面C1NB1;
(2)求二面角C-NB1-C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
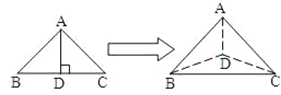
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC和平面ABC的垂直.
其中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2).(12分)
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ﹣3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在(μ﹣3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得 ![]() =
= ![]() =9.97,s=
=9.97,s= ![]() =
= ![]() ≈0.212,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
≈0.212,其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
用样本平均数 ![]() 作为μ的估计值
作为μ的估计值 ![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值 ![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除(
,利用估计值判断是否需对当天的生产过程进行检查?剔除( ![]() ﹣3
﹣3 ![]() +3
+3 ![]() )之外的数据,用剩下的数据估计μ和σ(精确到0.01).
)之外的数据,用剩下的数据估计μ和σ(精确到0.01).
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)=0.9974,0.997416≈0.9592, ![]() ≈0.09.
≈0.09.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B是椭圆C: ![]() +
+ ![]() =1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )
=1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )
A.(0,1]∪[9,+∞)
B.(0, ![]() ]∪[9,+∞)
]∪[9,+∞)
C.(0,1]∪[4,+∞)
D.(0, ![]() ]∪[4,+∞)
]∪[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知圆
中,已知圆![]() 圆心为
圆心为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(![]() )求
)求![]() 的取值范围;
的取值范围;
(![]() )是否存在常数
)是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com