
【题目】如图,在三棱柱![]() 中,底面
中,底面![]() 为正三角形,侧棱
为正三角形,侧棱![]() 底面
底面![]() .已知
.已知![]() 是
是 ![]() 的中点,
的中点,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:A1C∥平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)通过证明AD⊥平面BB1C1C,得出平面AB1D⊥平面BB1C1C;
(2)连接A1B,设A1B∩AB1=E,连接DE,易证 DE∥A1C,故而A1C∥平面AB1D;
(3)根据![]() 求出棱锥的体积
求出棱锥的体积
(1)证明:由已知![]() 为正三角形,且D是BC的中点,所以
为正三角形,且D是BC的中点,所以![]() .
.
因为侧棱![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .而
.而![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)证明:连接![]() ,设
,设![]() ,连接
,连接![]() .
.

由已知得,四边形![]() 为正方形,则
为正方形,则![]() 为
为![]() 的中点.
的中点.
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面AB1D,
平面AB1D,![]() 平面AB1D,所以A1C∥平面AB1D.
平面AB1D,所以A1C∥平面AB1D.
(3)由(2)可知A1C∥平面AB1D.,所以![]() 与
与![]() 到平面AB1D的距离相等,
到平面AB1D的距离相等,
所以![]() .
.
由题设及![]() ,得
,得![]() ,且
,且![]() .
.
所以![]()
![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() 为轨迹
为轨迹![]() 上异于原点
上异于原点![]() 的两点,且
的两点,且![]() .
.
①若![]() 为常数,求证:直线
为常数,求证:直线![]() 过定点
过定点![]() ;
;
②求轨迹![]() 上任意一点
上任意一点![]() 到①中的点
到①中的点![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①当![]() 时,有
时,有![]() ;
;
②若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ;
;
④函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
⑤当![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
的取值范围为![]() .
.
其中正确命题的序号为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+px+q.求证:
(1)f(1)+f(3)-2f(2)=2;
(2)|f(1)|,|f(2)|,|f(3)|中至少有一个不小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y2=2x与C2:y=![]() x2在第一象限内的交点为P.
x2在第一象限内的交点为P.
(1)求过点P且与曲线C2相切的直线方程;
(2)求两条曲线所围图形(如图所示的阴影部分)的面积S.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:
(1)AD应取多长?
(2)容器的容积为多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
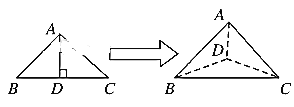
①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com