Question

2．若M是△ABC的边BC上一点，且$\overrightarrow{CM}=3\overrightarrow{MB}，设\overrightarrow{AM}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$，则λ的值为$\frac{3}{4}$．

Answer 1

分析 由题设CM：MB=3：1，过M作MN∥AC，交AB于N，则$\frac{BN}{BA}=\frac{BM}{BC}$=$\frac{1}{4}$，由此能求出λ的值．

解答 解：∵M是△ABC的边BC上一点，且$\overrightarrow{CM}$=3$\overrightarrow{MB}$，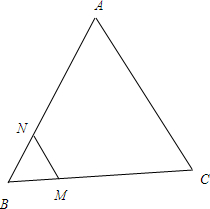
∴由题设CM：MB=3：1，
过M作MN∥AC，交AB于N，
则$\frac{BN}{BA}=\frac{BM}{BC}$=$\frac{1}{4}$，
从而$\frac{AN}{AB}$=$\frac{3}{4}$，
∵$\overrightarrow{AM}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$，
∴λ=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．

点评 本题考查实数值的求法，是中档题，解题时要认真审题，注意平面向量知识的合理运用．