
分析 利用勾股定理求出|BC|,得出cos∠ACB,代入向量的数量积公式计算.
解答 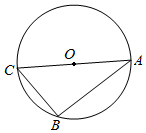 解:∵AC为圆O的直径,
解:∵AC为圆O的直径,
∴|$\overrightarrow{AO}$|=$\frac{1}{2}$|AC|=$\frac{\sqrt{7}}{2}$,|BC|=$\sqrt{|AC{|}^{2}-|AB{|}^{2}}$=$\sqrt{3}$.
∴cos∠ACB=$\frac{|BC|}{|AC|}$=$\frac{\sqrt{21}}{7}$.
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{\sqrt{7}}{2}×\sqrt{3}×\frac{\sqrt{21}}{7}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查额平面向量的数量积运算,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:选择题
| A. | 若l?α,m?α,l∥β,m∥β,则α∥β | |
| B. | 若l?α,m?β,l∥m,则α∥β | |
| C. | 若l?α,m?α,l∩m=点P,l∥β,m∥β,则α∥β | |
| D. | 若l∥α,l∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
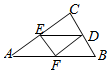 设D,E,F分别为△ABC的三边BC,CA,AB的中点,则$\overrightarrow{EC}$+$\overrightarrow{BF}$=( )
设D,E,F分别为△ABC的三边BC,CA,AB的中点,则$\overrightarrow{EC}$+$\overrightarrow{BF}$=( )| A. | $\frac{1}{2}$$\overrightarrow{BE}$ | B. | $\frac{1}{2}$$\overrightarrow{AD}$ | C. | $\overrightarrow{ED}$ | D. | $\overrightarrow{FE}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | (0,$\frac{1}{2}$] | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com