
分析 令函数g(x)=f(x)-$\frac{1}{2}$x,由题意可得g′(x)=f′(x)-$\frac{1}{2}$>0,即g(x)在R上递增,且g(3)=3,原不等式化为g(x2-2x)<g(3),运用单调性和二次不等式的解法即可得到解集.
解答 解:可设g(x)=f(x)-$\frac{1}{2}$x,
由对任意的实数x,f′(x)>$\frac{1}{2}$恒成立,可得
g′(x)=f′(x)-$\frac{1}{2}$>0,
即g(x)在R上递增,且g(3)=f(3)-$\frac{3}{2}$=$\frac{9}{2}$-$\frac{3}{2}$=3,
不等式f(x2-2x)<$\frac{1}{2}$(x2-2x)+3,
即为f(x2-2x)-$\frac{1}{2}$(x2-2x)<3,
即g(x2-2x)<g(3),
由g(x)在R上递增,可得x2-2x<3,
解得-1<x<3.
则解集为(-1,3).
故答案为:(-1,3).
点评 本题考查导数的运用:判断单调性,考查单调性的运用:解不等式,以及构造函数法,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
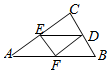 设D,E,F分别为△ABC的三边BC,CA,AB的中点,则$\overrightarrow{EC}$+$\overrightarrow{BF}$=( )
设D,E,F分别为△ABC的三边BC,CA,AB的中点,则$\overrightarrow{EC}$+$\overrightarrow{BF}$=( )| A. | $\frac{1}{2}$$\overrightarrow{BE}$ | B. | $\frac{1}{2}$$\overrightarrow{AD}$ | C. | $\overrightarrow{ED}$ | D. | $\overrightarrow{FE}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{3}}{2}$] | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | (0,$\frac{1}{2}$] | D. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1-($\frac{5}{6}$)5]100 | B. | [1-($\frac{5}{6}$)100]5 | C. | 1-[1-($\frac{1}{6}$)100]5 | D. | 1-[1-($\frac{1}{6}$)5]100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com