
���� ��1��ȷ���¼�A���ס��ҹ����30�����֣����¼�B���30�����֣��һ��0�����֣����¼�C�һ��30�����֣����0�����֣����û����¼��ĸ��ʹ�ʽ�ó�P��A��=P��B��+P��C�������Ϳ��ó��𰸣�
��2��ȷ���ο���ȡֵ0��5��10��30�������Ӧ�ĸ��ʣ��ó��ֲ��У�������ѧ������ʽ��⼴�ɣ�
��� �⣺��1�����¼�A���ס��ҹ����30�����֣����¼�B���30�����֣��һ��0�����֣����¼�C�һ��30�����֣����0�����֣�
����P��A��=P��B��+P��C����
��p��B��=��$\frac{2}{3}$��3����1-$\frac{1}{2}$��=$\frac{4}{27}$��P��C��=��1-$\frac{2}{3}$����$\frac{1}{2}��\frac{1}{2}��\frac{3}{4}$=$\frac{1}{16}$��
��P��A��=$\frac{4}{27}$$+\frac{1}{16}$=$\frac{91}{432}$��
��2���ο���ȡֵ0��5��10��30��
P����=0��=$\frac{1}{2}$��P����=5��=$\frac{1}{2}����1-\frac{1}{2}��$=$\frac{1}{4}$��
P����=10��=$\frac{1}{2}��\frac{1}{2}$��$��1-\frac{3}{4}��$=$\frac{1}{16}$��
P����=30��=$\frac{1}{2}��\frac{1}{2}��\frac{3}{4}$=$\frac{3}{16}$��
| �� | 0 | 5 | 10 | 30 |
| p | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{16}$ | $\frac{3}{16}$ |
���� ���⿼������ɢ�͵ĸ������⣬�ֲ�����ѧ������������ѧ�����Ķ�������������������ʵ�������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | ֱ�������� | ||
| C�� | �۽������� | D�� | ��ȷ�������ε���״ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | S7 | B�� | S4 | C�� | S13 | D�� | S16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
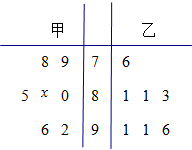 ij��ѧ�����꼶�Ӽס��������༶��ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ����ƽ������85��
ij��ѧ�����꼶�Ӽס��������༶��ѡ��7��ѧ���μ���ѧ����������ȡ�õijɼ�������100�֣��ľ�Ҷͼ��ͼ�����мװ�ѧ����ƽ������85���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 6 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��$\frac{��}{6}$����λ���� | B�� | ����ƽ��$\frac{��}{12}$����λ���� | ||
| C�� | ����ƽ��$\frac{��}{6}$����λ���� | D�� | ����ƽ��$\frac{��}{12}$����λ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com