
分析 根据同角的三角函数关系式进行化简,利用弦化切进行计算即可.
解答 解:$\frac{1}{cos2α}$+tan2α=$\frac{1}{cos2α}$+$\frac{sin2α}{cos2α}$=$\frac{1+sin2α}{cos2α}$=$\frac{(sinα+cosα)^{2}}{cos^2α-sin^2α}$=$\frac{sinα+cosα}{sinα-cosα}$=$\frac{1+tanα}{1-tanα}$,
∵$\frac{1+tanα}{1-tanα}$=2016,
∴$\frac{1}{cos2α}$+tan2α=2016,
故答案为:2016
点评 本题主要考查三角函数的化简和求值,利用同角的三角函数关系式进行化简是解决本题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | y=1+cos(2x+$\frac{π}{4}$) | B. | y=1-cos(2x+$\frac{π}{4}$) | C. | y=2-sin(2x-$\frac{π}{4}$) | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | $({-∞,\frac{1}{4}})$ | C. | $({\frac{1}{2},+∞})$ | D. | $({\frac{1}{4},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男性 | 女性 | 合计 | |
| 反感 | 10 | ||
| 不反感 | 8 | ||
| 合计 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
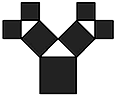 如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.
如图所示:一个边长为$\frac{{\sqrt{2}}}{2}$的正方形上连接着等腰直角三角形,等腰直角三角形的边上再连接正方形,…,如此继续.若共得到255个正方形,则最小正方形的边长为$\frac{1}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com