
分析 (1)将极坐标方程两边同乘ρ,去分母即可得到直角坐标方程;
(2)利用直线l参数方程的标准形式,代入曲线C的普通方程,根据参数的几何意义得出|AB|.
解答 解:(1)∵ρ=$\frac{6cosθ}{si{n}^{2}θ}$,∴ρ2sin2θ=6ρcosθ,
∴曲线C的直角坐标方程为y2=6x.曲线为以($\frac{3}{2}$,0)为焦点,开口向右的抛物线.
(2)直线l的参数方程为$\left\{\begin{array}{l}x=\frac{3}{2}+\frac{t}{2}\\ y=\frac{{\sqrt{3}t}}{2}\end{array}\right.$,代入y2=6x得t2-4t-12=0.
解得t1=-2,t2=6.
∴|AB|=|t1-t2|=8.
点评 本题考查了极坐标方程与直角坐标方程的转化,直线参数方程的几何意义,属于基础题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{11}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{5}{11}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
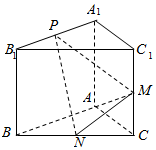 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ∈R).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{49}$ | B. | $\frac{12}{49}$ | C. | $\frac{6}{25}$ | D. | $\frac{4}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1]∪(3,+∞) | B. | [-1,3) | C. | (-∞,-1]∪[3,+∞) | D. | [-1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com