
分析 ①当$\overrightarrow{a}$=$\overrightarrow{0}$时,结论不成立,
②根据向量数量积的公式进行化简即可,
③根据向量投影的定义进行计算即可,
④根据向量加法和加法的几何意义进行判断即可.
解答  解:①当$\overrightarrow{a}$=$\overrightarrow{0}$时,满足$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,但$\overrightarrow{b}$=$\overrightarrow{c}$不一定成立,故①错误;
解:①当$\overrightarrow{a}$=$\overrightarrow{0}$时,满足$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,但$\overrightarrow{b}$=$\overrightarrow{c}$不一定成立,故①错误;
②若|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,则|$\overrightarrow{a}$|•|$\overrightarrow{b}$cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,即cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=|1,则<$\overrightarrow{a}$,$\overrightarrow{b}$>=180°|,即$\overrightarrow{a}$∥$\overrightarrow{b}$成立.故②正确,
③$\overrightarrow{a}$=(-1,1)在$\overrightarrow{b}$=(3,4)方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{-3+4}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{1}{5}$;故③正确,
④设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,
以OA OB为邻边,作平行四边形OACB,则 $\overrightarrow{OC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,∠AOC为$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角.
由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,可得△OAB 为等边三角形,故平行四边形OACB为菱形,
∴∠AOC=30°
则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为30°.故④错误,
故答案为:②③
点评 本题主要考查命题的真假判断,涉及平面向量的有关概念和运算,以及数量积的公式,考查学生的运算和推理能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
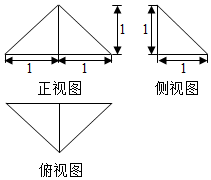
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
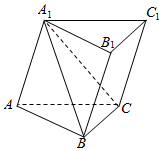 如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.
如图,三棱柱ABC-A1B1C1的体积为V1,四棱锥A1-BCC1B1的体积为V2,则$\frac{V_1}{V_2}$=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,点P是半径为1的半圆弧$\widehat{AB}$上一点,若AP长度为x,则直线AP与半圆弧$\widehat{AB}$所围成的面积S关于x的函数图象为( )
如图,点P是半径为1的半圆弧$\widehat{AB}$上一点,若AP长度为x,则直线AP与半圆弧$\widehat{AB}$所围成的面积S关于x的函数图象为( )| A. | 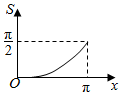 | B. | 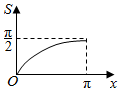 | C. | 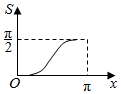 | D. | 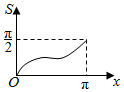 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(ln2)>2f(ln3) | B. | 3f(ln2)=2f(ln3) | ||
| C. | 3f(ln2)<2f(ln3) | D. | 3f(ln2)与2f(ln3)的大小不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com