
分析 由题意A1,A2,A3是两两互斥的事件,由条件概率公式求出P(B|A1),P(B)=P(A1B)+P(A2B)+P(A3B),对照四个命题进行判断找出正确命题,选出正确选项.
解答 解:由题意A1,A2,A3是两两互斥的事件,P(A1)=$\frac{5}{10}$=$\frac{1}{2}$,P(A2)=$\frac{2}{10}$=$\frac{1}{5}$,P(A3)=$\frac{3}{10}$,
P(B|A1)=$\frac{P(B{A}_{1})}{P({A}_{1})}$=$\frac{\frac{5}{11}×\frac{1}{2}}{\frac{1}{2}}$=$\frac{5}{11}$,
由此知,②错误;
P(B|A2)=$\frac{4}{11}$,P(B|A3)=$\frac{4}{11}$;
而P(B)=P(A1B)+P(A2B)+P(A3B)
=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)=
$\frac{1}{2}$×$\frac{5}{11}$+$\frac{1}{5}$×$\frac{4}{11}$+$\frac{3}{10}×\frac{4}{11}$+$\frac{3}{10}×\frac{4}{11}$=$\frac{9}{22}$,
由此知①正确,③错误.
∵A1,A2,A3是两两互斥的事件,由此知④正确;
对照四个命题知①④正确;
故答案为:①④.
点评 本题考查相互独立事件,解题的关键是理解题设中的各个事件,考查相互独立事件的概率简洁公式,条件概率的求法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
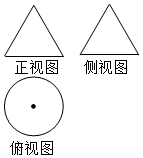 某几何体的三视图如图所示,其中正视图和俯视图都是腰长为2的等腰三角形,俯视图是半径为1的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中正视图和俯视图都是腰长为2的等腰三角形,俯视图是半径为1的圆,则该几何体的表面积是( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
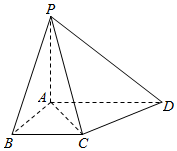 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-2,或a>0 | B. | 0<a<1 | C. | 1<a<3 | D. | 2<a<6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
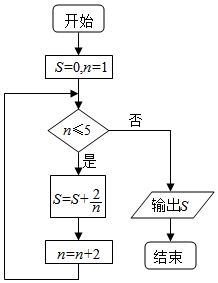
| A. | 2.$\stackrel{•}{6}$ | B. | 3.0$\stackrel{•}{6}$ | C. | 4.1$\stackrel{•}{6}$ | D. | 4.5$\stackrel{•}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com