
分析 根据三角函数的图象平移关系求出函数g(x)的解析式进行求解即可.
解答 解:将函数f(x)=cos2x的图象横坐标不变纵坐标伸长到原来的2倍,
得到y=2cos2x,
再向左平移$\frac{π}{6}$个单位后,得到y=2cos2(x+$\frac{π}{6}$),
即g(x)=2cos2(x+$\frac{π}{6}$),
则g($\frac{π}{6}$)=2cos2($\frac{π}{6}$+$\frac{π}{6}$)=2cos$\frac{2π}{3}$=-2cos$\frac{π}{3}$=$-2×\frac{1}{2}$=-1,
故答案为:-1.
点评 本题主要考查三角函数值的计算,利用三角函数的图象变换关系求出函数的解析式是解决本题的关键.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
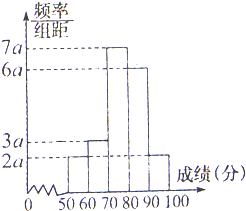 200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:
200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{3}{2}π,π]$ | B. | $[\frac{5}{2}π,3π]$ | C. | $[-\frac{5}{6}π,-\frac{π}{2}]$ | D. | $[-\frac{1}{2}π,\frac{5π}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{3}$,$\frac{1}{3}$) | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | ($\frac{2}{3}$,$\frac{4}{3}$) | D. | [$\frac{2}{3}$,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
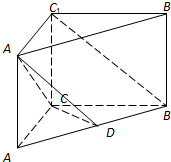 如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com