
| A. | 3 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\frac{13}{3}$ |
分析 利用平面向量的计算法则求得a的值;然后结合正弦定理来求△DBC的面积.
解答 解:∵$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BD}$=$\frac{\sqrt{17}}{2}$,
∴$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\frac{\sqrt{17}}{2}$,
两边平方得$\frac{1}{4}$(4+2×2-$\frac{1}{3}$a+a2)=$\frac{17}{4}$,即3a2+4a-39=0,
解得a=-$\frac{13}{3}$(舍去)或a=3.
∴S△ABC=$\frac{1}{2}$AB•BC•sinB=$\frac{1}{2}$×2×3×$\sqrt{1-\frac{1}{9}}$=2$\sqrt{2}$,
∴S△DBC=$\frac{1}{2}$S△ABC=$\sqrt{2}$,
故选:B.
点评 本题考查三角形的正弦定理和平面向量的加法运算的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {3,4,5} | B. | {x|2<x<6} | C. | {x|3≤x≤5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
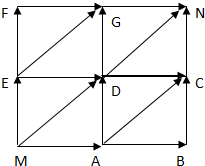 某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:
某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:| 从M到N用的步数 | 2 | 3 | 4 |
| 奖励金额(元) | 100 | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x}$与y2=x | B. | y=x与$\frac{x}{y}=1$ | C. | y2-x2=0与|y|=|x| | D. | y=x0与y=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [4,+∞) | C. | (0,4] | D. | (1,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com